Analyze the performance of Google PageRank algorithm
“d”是一个阻尼因子，通常在0.85左右，这意味着用户在点击了一系列链接后将停止冲浪。您将使用迭代算法来找到以下问题的解决方案： 上述递推方程。在该算法中，我们从顶点的一些初始秩值开始，然后用上述方程迭代修正它们。
在项目的第一部分，您将实现这个算法，该算法的输入将包括(I)一个有向图，(Ii)一个阻尼因子，(C)迭代限制和(D)误差限制。你 如果新的秩值与上一次迭代中的值在误差范围内不同，或者迭代次数超过迭代限制，则将终止该算法。在后一种情况下 我们认为没有解决办法。对于每个顶点的秩，可以从初始值1/n开始。您应该有自己的算法实现(不是从任何网站或f借来的)。 其他人)。
项目的第二部分要求您编写一个程序来测试该算法的性能。对于顶点数“n”和最大出度(n的%)的各种值，您需要g。 产生随机的图形输入。这些图是通过翻转一个硬币来决定在最大外度约束下，顶点u到顶点v是否应该有一个边。对于每个 这些图表，运行您的算法，如果有解决方案，将它包含在您将用于评估性能的时间统计中。对于n的每个值和最大出度，生成多个i。 NPUT病例来衡量平均时间。
您应该将平均时间绘制为所选择的每个最大输出度值(n%)的顶点数的函数。
您应该用C或Java(更好)实现它。对于Java，提交一个包含(A)源代码、(B)包含.class文件的Jar文件和(C)一个我可以运行的Windows命令文件的zip文件 o执行测试程序并以表格形式查看性能结果；(D)关于算法如何渐近执行的结果的一页总结。对于C，而不是(B)，su bmit可以在AFS UNIX主机上运行的可执行文件，以及用于(C)提交UNIXshell脚本来运行测试程序的可执行文件。
The goal of this project is to analyze the performance of Google PageRank algorithm which we will discuss in detail in the class when we discuss graphs. This algorithm assigns a rank to a web page based on how often a web user can arrive at a page clicking on links from other pages. Higher the rank of a web page higher its relevance which the search engine can use in displaying the results of a search.
PageRank is probability function defined as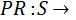 
[0, 1] where S is the set of web pages of interest and 
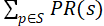= 1. Let every page in S be represented as a vertex in a directed graph (S, E) where edge (u, v) indicates there is a link from page u to page v. Then the rank function satisfies the relation:
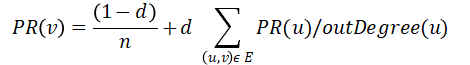
“d” is a damping factor usually around 0.85 which indicates that the user will stop surfing after clicking through some series of links. You will be using an iterative algorithm to find a solution to the above recurrence equations. In this algorithm we start with some initial rank values for the vertices and then modify them iteratively using the above equation.
In the first part of the project you will be implementing this algorithm for which the input will consist of (i) a directed graph, (ii) a damping factor, (c) iteration limit and (d) error limit. You will terminate the algorithm if either the new rank values differ from values in the previous iteration within the error limit or the number of iterations exceeds the iteration limit. In the latter case we will deem there is no solution. You can start with initial value of 1/n for the rank of each vertex. You should have your own implementation of this algorithm (not borrowed from any web site or from anyone else).
Second part of the project requires you to write a program to test the performance of this algorithm. For various values of the number of vertices “n” and maximum out-degree (as % of n), you need to generate random graphs as inputs. These graphs are generated by flipping a coin to determine if there should be an edge from a vertex u to vertex v within the maximum out-degree constraint. For each of these graphs, run your algorithm and if there is a solution, include it in the time statistics that you will use to assess the performance. For each value of n and maximum out-degree, generate many input cases to measure the average time.
You should plot the average time as a function of number of vertices for each maximum out-degree value (% of n) that you have selected.
You should implement it in either C++ or Java (preferable). For Java, submit a zip file containing (a) source code, (b) Jar file containing .class files and (c) a Windows command file that I can run to execute the test program and see the performance results in a tabular form and (d) one-page summary of your findings regarding how the algorithm performs asymptotically . For C++, instead of (b), submit the executables that can be run on an AFS UNIX host and for (c) submit UNIX shell script to run the test program.
