在R中模仿存储问题
本例来自于《统计模子及其R实现》的例题,可是书上的条件和代码都有些缺漏,所以仍值得在这里说道说道。存储模子是很经典的统计模仿问题,即思量一个出售某种商品的商店,其销售单价为12元,单元本钱为5元。顾主数听从参数为8的Poisson漫衍,且每个顾主的需求量是一个离散随机变量。东家必需储存必然的商品,当库存不敷时,东家就会从发货商处获得增补。利用的订货计策即(s,S)计策,若当前库存x小于s时,则将存货增补到S,即购置S-x个单元商品。每次进货本钱为10元,进货延迟时间为2天,单元时间内库存一个商品的本钱是0.5元,若需求量大于当前存货,则产生损失。思量30天之内的时间长度,东家可以或许决定的变量等于再订货点s和订货数量S。总本钱包罗了订货本钱、存储本钱和损失用度,要思量如何抉择这两个变量值,才气使平均收入(总收入除以30天)到达较大?
办理问题的思路是先成立一个存货函数,输入参数为s和S,输出量为平均收入。然后生成多个输入参数的组合,对每个参数组合运行函数100次获得平均收入的均值。最后调查哪一组参数可以获得较大的平均收入均值。由于这实际上是一个二元函数,所以可以用lattice包中的三维画图函数获得一个直观的图形,显示如下。
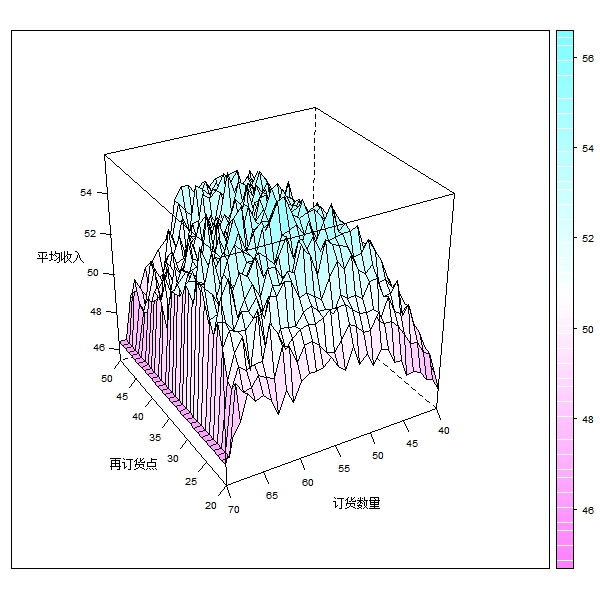
我们也可以利用二维热图来暗示这个函数之间的干系,从下图看到显示的蓝色区域越深,即为平均收入较高的参数组合,大抵位置在中部偏左下方。
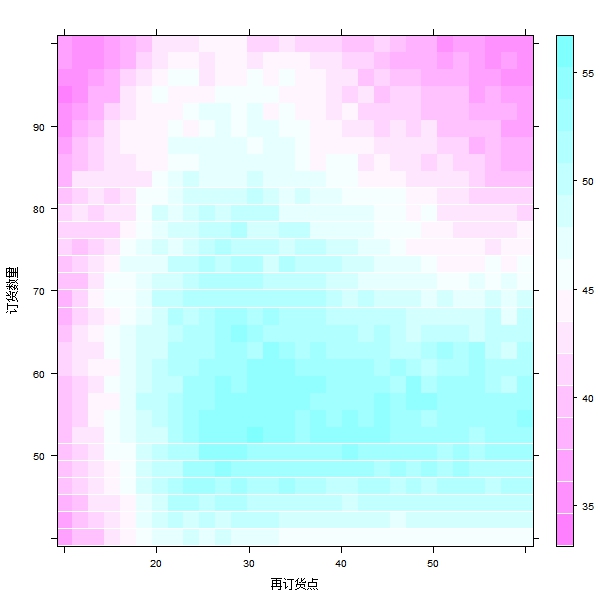
最后我们来看看平均收入前十个的参数组合,以较高的组合为例,即当今朝存货低于29时,我们需要将存货增补到57,也就是说订购28个存货。此时我们的平均收入的均值将为55.85元。
| 再订货点 | 订货数量 | 平均收入 |
| 29 | 57 | 55.85 |
| 32 | 57 | 55.74 |
| 29 | 58 | 55.71 |
| 27 | 52 | 55.41 |
| 31 | 57 | 55.33 |
| 30 | 54 | 55.29 |
| 32 | 61 | 55.29 |
| 30 | 56 | 55.22 |
| 35 | 56 | 54.99 |
| 36 | 56 | 54.97 |
由于模子的随机性,所以55.85只是期望意义上的平均收入,假如碰着某些极度环境,平均收入会有颠簸。为了调查这种变异性,我们可以以(29,57)为输入参数,将函数运行1000次,获得1000个平均收入。最后绘制直方图举办调查。可以看到大部门环境下平均收入会在40元到65元阁下。
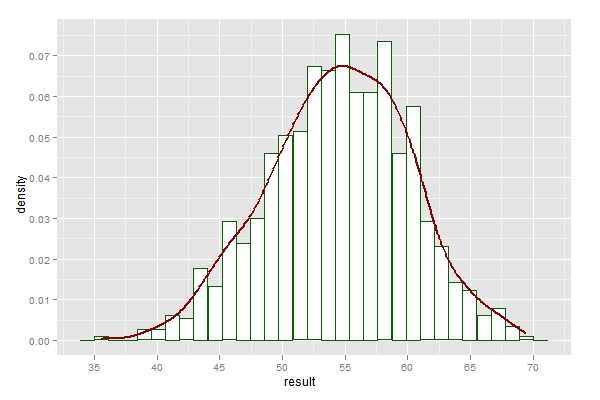
R代码如下:
rm(list=ls())
inventory = function(s,S) {
#x为存货,T为总时长,lambda为需求速率,(s,S)为存货计策
#h为单元库存用度,L为订货周期,d为订货用度函数,lose为损失函数
#a为需求量,b为相应的概率
x=4; L=2; h =0.5
r=12; a=1:4; b=c(0.7,0.2,0.08,0.02)
lambda=8; T=30
d = function(x) 10+ 5*x
lose = function(D,x) (D-x)*2
# t0为下一个顾主达到时间,听从指数漫衍,t1为订货交付时间
#若没有订货则设为Inf,H为累积库存用度,C为累积订货用度,R为收入
#y为存货订货量,loss为损失金额,k为计数
t=0; t0=rexp(1,lambda)
t1=Inf; H=0; C=0; R=0; y=0
loss=0; k=1
while(t0[k] <= T) {
# browser()
k = k+1
if (t0[k-1] < t1[k-1]) {
#计较t时到下一个顾主到来时的库存用度
H= H + (t0[k-1] – t) * h*x
t = t0[k-1]
#D为模仿的顾主需求量,w为购置量
D = sample(a,1,prob=b)
w = min(D,x)
#需求大于存货,则产生损失
if (D > x) { loss[k-1]=lose(D,x) }
else {loss[k-1] =0 }
# 计较收入并更新存货
R = R + w*r; x=x-w
# 若存货不敷则举办订货增补,到货时间为t1。
if(x <s & y==0) {
y = S-x; t1[k] = t +L
} else { t1[k]= t1[k-1]}
# 模仿新的顾主需求
t0[k]=t+rexp(1,lambda)
loss[k] =0
# 若新的存货比需求先达到,则计较订货本钱并更新存货
} else {
H= H + (t1[k-1]-t)*h*x
t=t1[k-1]
C=C+d(y); x=x+y
y=0;t1[k]= Inf; loss[k]=0; t0[k]= t0[k-1]
}
}
return((R-H-C-sum(loss))/T)
}library(lattice)
s <- 20:50
S <- 40:70
data <- expand.grid(s,S)
for (i in 1:900) {
data$mean[i] <- mean(replicate(100,inventory(data$Var1[i],data$Var2[i])))
}
wireframe(mean ~ Var1 * Var2, data = data,
scales = list(arrows = FALSE),xlab = “再订货点”,
ylab = “订货数量”, zlab=’平均收入’,
drape = TRUE, colorkey = TRUE,
screen = list(z = 120, x = -60))
levelplot(mean ~ Var1 * Var2, data = data,xlab = “再订货点”,
ylab = “订货数量”)data[order(data$mean,decreasing=T)[1:10],]
result <- replicate(1000,inventory(29,57))
library(ggplot2)
p <- ggplot(data.frame(result),aes(x=result))
p+geom_histogram(colour = “darkgreen”, fill = “white”,
aes(y = ..density..)) +
stat_density(geom = ‘line’,colour=’red4′,size=1)
