R语言与数据的预处理惩罚

在面临大局限数据时，对数据预处理惩罚，获取根基信息是十分须要的。本日分享的就是数据预处理惩罚的一些对象。

一、获取重要数据

在导入大局限数据时，我们凡是需要知道数据中的要害内容：最值，均值，离差，分位数，原点矩，离差，方差等。在R中常用的函数与浸染整理如下：

统计函数	浸染
Max	返回数据的较大值
Min	返回数据的最小值
Which.max	返回较大值的下标
Which.min	返回最小值的下标
Mean	求均值
Median	求中位数
mad	求离差
Var	求方差（总体方差）
Sd	求尺度差
Range	返回【最小值，较大值】
Quantile	求分位数
Summary	返回五数归纳综合与均值
Finenum	五数归纳综合（最值，上下四分位数，中位数）
Sort	排序（默认升序，decreasing=T时为降序）
Order	排序（默认升序，decreasing=T时为降序）
Sum	求和
length	求数据个数
emm	Actuar包中求k阶原点矩
skewness	Fbasic包中求偏度
kurtosis	Fbasics包中求峰度

注：工具为分组数据，矩阵时返回的不是整体的方差，均值，而是每一列（组）的方差均值其余变量雷同。

二、直方图与频数统计

对付数据漫衍的认识，在大局限时有须要利用直方图。在R语言中，直方图的函数挪用为：

hist(x, breaks = “Sturges”,

freq = NULL, probability = !freq,

include.lowest = TRUE, right = TRUE,

density = NULL, angle = 45, col = NULL, border = NULL,

main= paste(“Histogram of” , xname),

xlim = range(breaks), ylim = NULL,

xlab = xname, ylab,

axes = TRUE, plot = TRUE, labels = FALSE,

nclass = NULL, warn.unused = TRUE, …)

这里值得一提的是，分组参数breaks默认利用史特吉斯（Sturges）公式，按照测定命n 来计较组距数k，公式为：k＝1+3.32 logn。虽然也可以本身设定一个数组来抉择分组。（举例拜见《R语言画图进修条记》）

说完频率漫衍直方图，我们尚有频率漫衍直方表。对付数据的统计，函数table可以统计出数据中完全沟通的数据个数。譬喻对《全宋词》中暴力拆解（两个相邻字算一词）词语利用数目标统计措施如下：

[plain] view plaincopyprint?

l=scan(“Ci.txt”,”character”,sep=”\n”);
l.len=nchar(l);
ci=l;
sentences=strsplit(ci,”，|。|！|？|、”);# 句子用标点标记支解。
sentences=unlist(sentences);
sentences=sentences[sentences!=””];
s.len=nchar(sentences);#单句太长了说明有大概是错误的字符，去除去。
sentences=sentences[s.len<=10];
s.len=nchar(sentences);
splitwords=function(x,x.len)substring(x,1:(x.len-1),2:x.len);
words=mapply(splitwords,sentences,s.len,SIMPLIFY=TRUE,USE.NAMES=FALSE);
words=unlist(words);
words.freq=table(words);#词频统计
words.freq=sort(words.freq,decreasing=TRUE);
data.frame(Word=names(words.freq[1:100]),Freq=as.integer(words.freq[1:100]));

#p#分页标题#e#

而对付一堆数，我们按区间做的时候，就还需要函数cut.挪用名目如下：

cut(x, breaks, labels = NULL,

    include.lowest = FALSE, right = TRUE, dig.lab = 3,

    ordered_result = FALSE, ...)

举一个具编制子，某一款保险产物，假设保单达到的速率为10张/天，理赔产生的速率为
1次/天。假设每张保单价值c=120，理赔额听从参数为v=1/1000
(以c*lambda1=1.2*lambda2/v设定)的指数漫衍。设定初始u=3000时，计较到第1000天为止产生破产的概率。（案例摘自《复
合泊松进程模子的推广和在R语言情况下的随机模仿》）

破产进程的R代码如下：

[plain] view plaincopyprint?

pois.proc= function(T, lambda){
S = 0
I =rpois(1, lambda*T) #发生t 泊松漫衍，这里挪用R 内置的泊松函数制止轮回。
U =runif(I)
S =sort(T * U) #排序发生顺序统计量的思想
list(I= I, S = S)
}
broken.proc= function(k, u= 3000, c= 120){
n =1000 #模仿到时刻 1000 为止的破产环境
M =pois.proc(n, 10)
N =pois.proc(n, 1)
U = u #初始盈余
X = 0
result=0
A =sort(c(M$S, N$S)) #M$S和 N$S 是保单和理赔到达时刻
for(iin 1:length(A)){
if(any(A[i]==N$S)== 0)
U=U+c
else {
X[i] =rexp(1, rate=1/1000)
U = U -X[i] #减去这个随机值
if(U< 0){ #判定盈余是否小于0（保单达到的时候不需要判定）
result<-A[i] #盈余小于 0时，记录这个理赔达到（破产）的刻
break}
}
}
if(U>= 0){ #假如 for轮回没有间断，判最终的盈余其实必定非负
result= n + 200
} #给功效赋值一个明明比模仿时刻大的数据，暗示未破产
return(result) #返回最终功效
}
#按照这个破产进程可以模仿保险人的频数和频率：
simulation= function(n=100){ #界说一个反复模仿破产进程的函数
t =numeric(n)
for(iin 1:n){
t[i] =broken.proc(i)} #发生 n次破产可能代表未破产的时刻
return(t)}
time=simulation(n= 1200)
rangetime= time[time!=1200]
breakratio= length(rangetime)/length(time);
breakratio
break.points<-c(0,10,20,30,40,50,100,200,300,400,500,1000,1200)
table(cut(time,breaks=break.points))
hist(rangetime,breaks = 50, xlab=’broken time’,xlim = c(0, max(rangetime)),main = ‘Histogramof Broken time’)

#p#分页标题#e#

用R 语言模仿了1200 次，最终功效 1200 次中破产 628 次，破产率或许 52.3% 。输出各阶段破产时刻频数和率功效如下：

区间	频数
(0,10]	389
(10,20]	89
(20,30]	45
(30,40]	28
(40,50]	16
(50,100]	36
(100,200]	17
(200,300]	6
(300,400]	2
(400,500]	0
(500,1000]	0
(1000,1200]	572

对付一些数据我们大概直接录入的是频率漫衍直方表，那么actuar包中提供了一个有用的数据布局grouped.data。挪用名目：

grouped.data(..., right = TRUE, row.names = NULL, check.rows = FALSE,

             check.names = TRUE)

运用举例：

#p#分页标题#e#

[plain] view plaincopyprint?

library(actuar)
z=rnorm(10000)
break.points<-c(-Inf,-3,-2,-1,0,1,2,3,Inf)
tz<-table(cut(z,breaks=break.points))
tz
zz<-grouped.data(Group=break.points,freq=as.matrix(tz))
zz

比拟一下下面的输出功效，我们发明分组数据的均值计较与总体数据计较要领是纷歧样的。

[plain] view plaincopyprint?

mean(zz)
mean(zz[c(2:7),])
mean(z)

注：函数elev()可以计较有限期望值，可以制止mean（zz）不存在的难过。

虽然对付数据的直观阐明R提供的函数有很多，我们将常见的函数汇总如下：

[plain] view plaincopyprint?

EDA <- function (x)
{
par(mfrow=c(2,2)) # 同时做4个图
hist(x) # 直方图
dotchart(x) # 点图
boxplot(x,horizontal=T) # 箱式图
qqnorm(x);qqline(x) # 正态概率图
par(mfrow=c(1,1)) # 规复单图
}

三、正态检讨与履历漫衍

对付数据的漫衍预计履历漫衍是一个很是好的预计。在actuar包中函数ogive给出的实现：

ogive(x, y = NULL, ...)

## S3 method for class 'ogive'

print(x, digits = getOption("digits") - 2, ...)

## S3 method for class 'ogive'

summary(object, ...)

## S3 method for class 'ogive'

knots(Fn, ...)

## S3 method for class 'ogive'

plot(x, main = NULL, xlab = "x", ylab = "F(x)", ...)

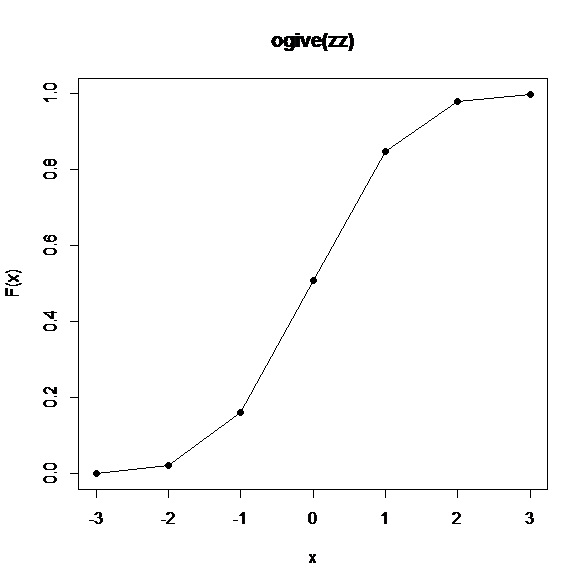
照旧以上面的例子数据zz为例：

ogive(zz)

plot(ogive(zz))

输出功效：

Ogive forgrouped data

Call:ogive(zz)

x = -Inf, -3, -2, …, 3, Inf

F(x) = 0, 0.0011, 0.0229, …,0.9985, 1

R语言与数据的预处理惩罚处罚

由于大数定律的存在，许多环境下，正态性检讨是十分有须要的一个漫衍检讨，在R中提供的正态性检讨可以汇总为下面的一个正态检讨函数：

#p#分页标题#e#

[plain] view plaincopyprint?

NormTest<-function(data){
library(fBasics)
library(nortest)
udata<-unique(data)
result<-list()
result$D<-dagoTest(data)
result$jB<-jarqueberaTest(data)
result$SW<-shapiroTest(data)
result$lillie<-lillie.test(data)
result$ad<-ad.test(data)
result$cvm<-cvm.test(data)
result$sf<-sf.test(data)
return(result)
}

对付漫衍的检讨尚有卡方检讨，柯尔莫哥洛夫检讨等，在R中也有实现函数chisq.test()等。我们同样以一个例子来说明：

R语言与数据的预处理惩罚处罚

例子摘自：王兆军《数理统计教材》习题6.3

解答如下：（功效以注释形式标明）

[plain] view plaincopyprint?

v<-c(57,203,383,525,532,408,273,139,45,27,16)
chisq.test(v)#p<0.05,认为检讨总体是否与给定的p沟通，p缺省暗示等大概性检讨
#验证V的漫衍是否为poission漫衍
x<-0:10
options(digits=3)
likely<-function(lamda=3){
-sum(y*dpois(x,lamda=lamda,log=T))
}
library(stats4)
mle(likely)
chisq.fit<-function(x,y,r){
options(digits=4)
result<-list()
n<-sum(y)
prob<-dpois(x,3.87,log=F)
y<-c(y,0)
m<-length(y)
prob<-c(prob,1-sum(prob))
result$chisq<-sum((y-n*prob)^2/(n*prob))
result$p.value<-pchisq(result$chisq,m-r-1,lower.tail=F)
result
}
chisq.fit(x,v,1)#p<0.05 拒绝假设漫衍

当前位置：以往代写 > 其他教程 >R语言与数据的预处理惩罚