纯真形法求解一般线性筹划和对偶线性筹划问题

这个package做的是线性筹划问题的求解

一、问题配景

问题一：

企业（厂商）出产打算问题：

某企业操作三种原料B1、B2、B3出产A1、A2两种商品。三种原料的月供给量（吨），出产一吨产物A1，A2所需要各类原料的数量以及单元产物的价值（万元/吨）如表所示。那么该企业应如何布置出产打算，使总收益较大？

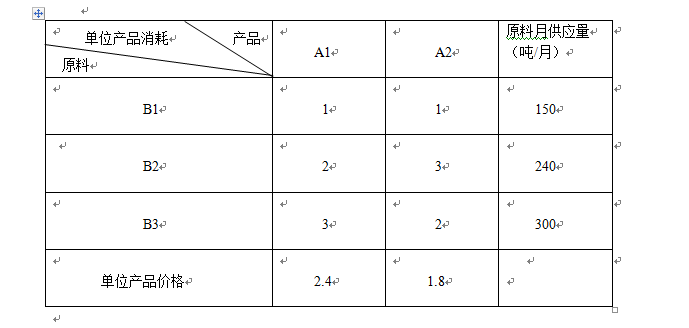
解：  设出产产物 Ai的数量为 xi（吨/月），i = 1,2，则按照原料的限制可以获得以下不等式组：

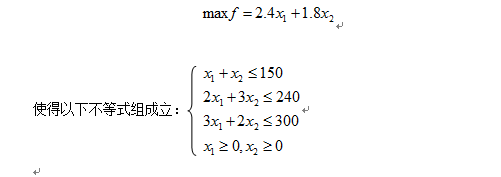
办理这类问题用到纯真形法，用simplex包里的lpsimplex函数即可办理。

    对问题举办进一步扩展，假如另一个公司想从该企业购置这三种原料，那么这三种原料的价值应是几多，双刚刚气都是公道的呢？

    设原料B1，B2，B3的价值为y1，y2，y3（万元/吨），显然，应有 yi>=0，i=1,2,3,。由原问题的条件，出产一吨产物A1, 需耗损1吨原料B1，2吨原料B2, 3吨原料B3，可得到收益为2.4万元。

     因此若将出产一吨产物A1的这些原料卖出所得的收益为y1+2*y2+3*y3(万元)，它必需不少于出产一吨产物A1所得的收益，对付该企业才是合算的。所以应有  y1+2*y2+3*y3   

    对付产物A2，可雷同获得y1+3*y2+2*y3  

    同时，若买方欲购置该工场的全部原料，则应支付150*y1+240*y2+300*y3万元（这也是该工场卖出全部原料的总收益）。从买方角度应使总支出尽大概少。因此，可获得线性筹划问题

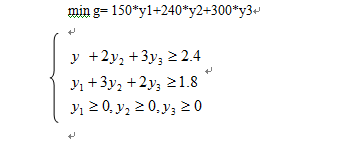
显然，这与前述问题互为对偶问题，可操作simplex包中的dualsimplex函数求解。

二.函数利用

1.函数语法：

lpsimplex(A,N)   A为按照各系数成立的纯真形表，N为初始基变量下标。

dualsimplex(c,A,b)  A为按照各系数成立的纯真形表，c为f的系数，b为常数项系数。

2.利用举例：

针对上述问题举办求解。

问题一，按照方程构成立纯真性表,利用lpsimplex求解

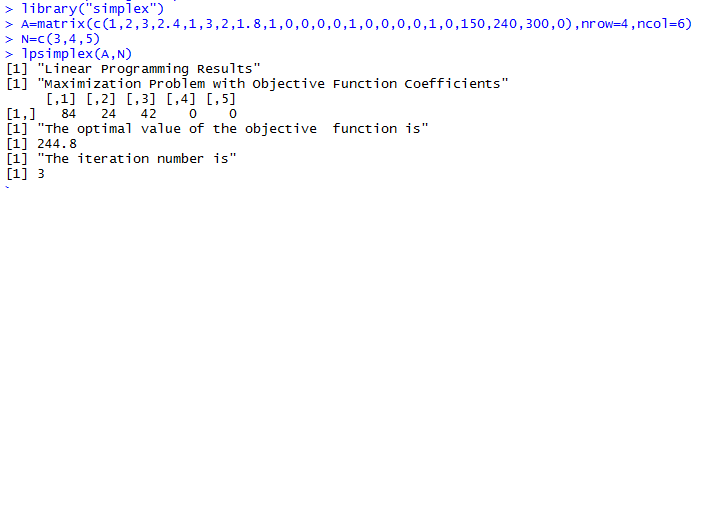
从函数运行功效可看到，问题一的最优解为x1=84,x2=24,败坏变量x3=42，表白原料B1尚有42吨未被利用，最优值为f=244.8，迭代次数为3次。

问题二，利用dualsimplex函数举办对偶线性筹划求解。

从运行功效可看出，对偶问题的最优解y1=0,y2=0.12,y3=0.72 最优值为g=244.8

详细内容可看辅佐文件。

simplex_1.0.zip

simplex_1.0.tar.gz

simplex包辅佐说明.pdf