用R语言做时间序列阐明（附数据集和源码）
时间序列（time series）是一系列有序的数据。凡是是等时距离断的采样数据。假如不是等隔断，则一般会标注每个数据点的时间刻度。
下面以time series 普遍利用的数据 airline passenger为例。 这是十一年的每月搭客数量，单元是千人次。
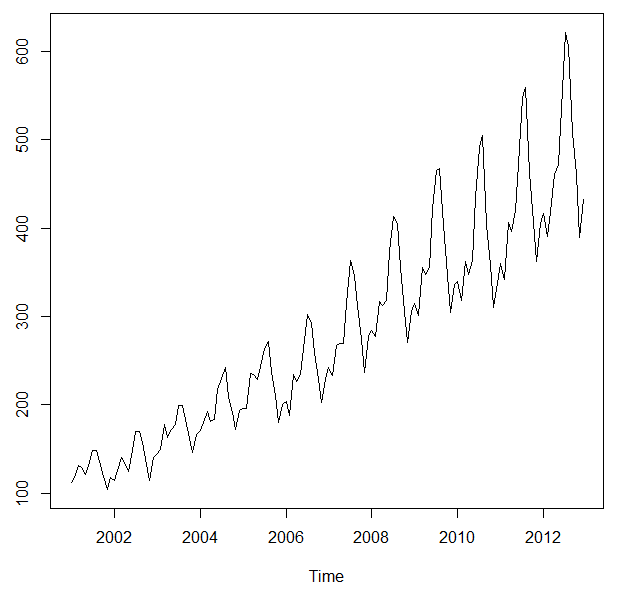
假如想实验其他的数据集，可以会见这里： https://datamarket.com/data/list/?q=provider:tsdl
可以很明明的看出，airline passenger的数据是很有纪律的。
time series data mining 主要包罗decompose（阐明数据的各个身分，譬喻趋势，周期性），prediction（预测将来的值），classification（对有序数据序列的feature提取与分类），clustering（相似数列聚类）等。
这篇文章主要接头prediction（forecast，预测）问题。 即已知汗青的数据，如何精确预测将来的数据。
先从简朴的要领说起。给定一个时间序列，要预测下一个的值是几多，最简朴的思路是什么呢？
（1）mean（平均值）：将来值是汗青值的平均。
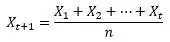
（2）exponential smoothing （指数衰减）：当去平均值得时候，每个汗青点的权值可以纷歧样。最自然的就是越近的点赋予越大的权重。
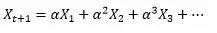
可能，更利便的写法，用变量头上加个尖角暗示预计值
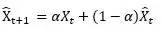
（3) snaive ： 假设已知数据的周期，那么就用前一个周期对应的时刻作为下一个周期对应时刻的预测值
（4） drift：飘移，即用最后一个点的值加上数据的平均趋势
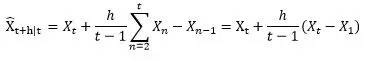
先容完最简朴的算法，下面开始先容两个time series内里最火的两个强大的算法： Holt-Winters 和 ARIMA。 上面简答的算法都是这两个算法的某种特例。
（5）Holt-Winters： 三阶指数滑腻
Holt-Winters的思想是把数据解析成三个身分：平均程度（level），趋势（trend），周期性（seasonality）。R内里一个简朴的函数stl就可以把原始数据举办解析：
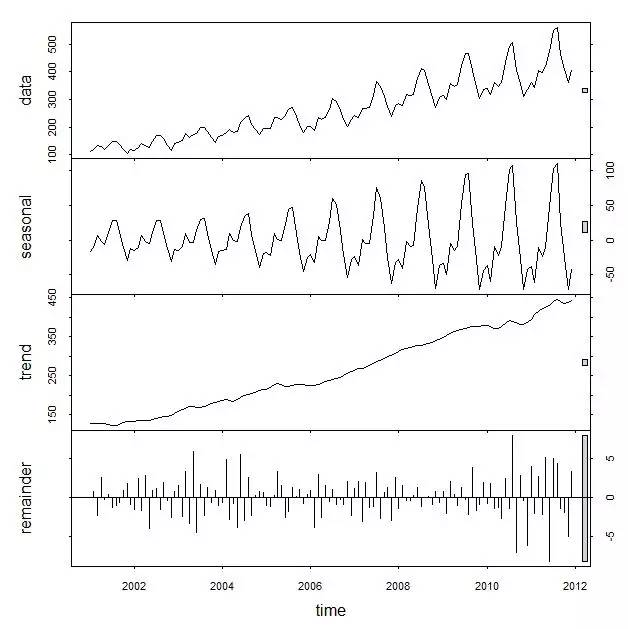
一阶Holt—Winters假设数据是stationary的（静态漫衍），等于普通的指数滑腻。二阶算法假设数据有一个趋势，这个趋势可以是加性的(additive,线性趋势)，也可以是乘性的(multiplicative,非线性趋势)，只是公式内里一个小小的差异罢了。 三阶算法在二阶的假设基本上，多了一个周期性的身分。同样这个周期性身分可以是additive和multiplicative的。 举个例子，假如每个二月的人数都比往年增加1000人，这就是additive；假如每个二月的人数都比往年增加120%，那么就是multiplicative。
R内里有Holt-Winters的实现，此刻就可以用它来试试结果了。我用前十年的数据去预测最后一年的数据。 机能权衡回收的是RMSE。 虽然也可以回收此外metrics：
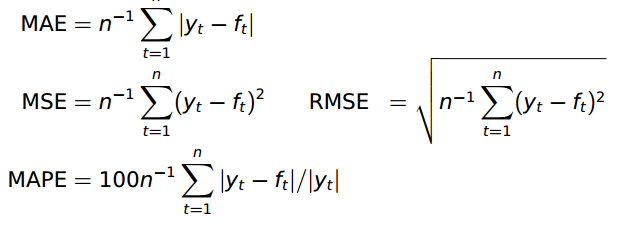
预测功效如下：
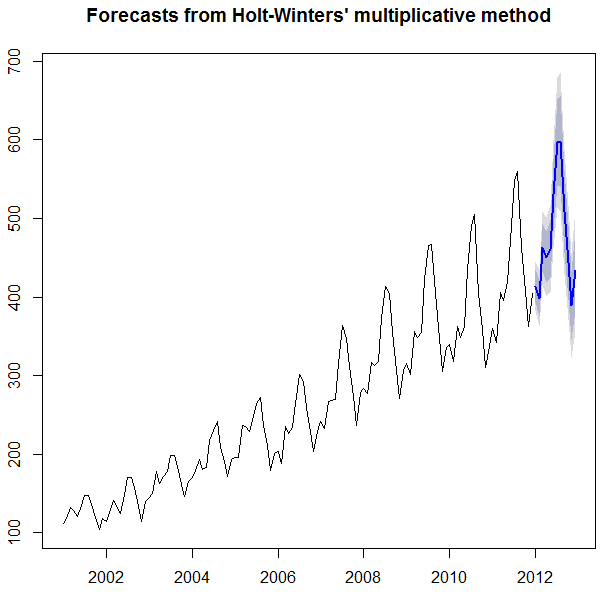
功效照旧很不错的。
（6） ARIMA： AutoRegressive Integrated Moving Average
ARIMA是两个算法的团结：AR和MA。其公式如下：
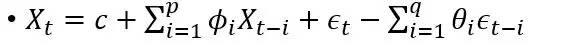
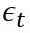是白噪声，均值为0， C是常数。 ARIMA的前半部门就是Autoregressive： 
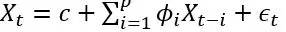，后半部门是moving average：
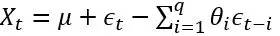。 AR实际上就是一个无限脉冲响应滤波器（infinite impulse resopnse）, MA是一个有限脉冲响应（finite impulse resopnse），输入是白噪声。
ARIMA内里的I指Integrated（差分）。 ARIMA（p,d,q）就暗示p阶AR，d次差分，q阶MA。 为什么要举办差分呢？ ARIMA的前提是数据是stationary的，也就是说统计特性（mean，variance，correlation等）不会跟着时间窗口的差异而变革。用数学暗示就是连系漫衍沟通：
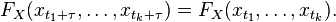
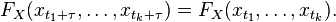
虽然许多时候并不切合这个要求，譬喻这里的airline passenger数据。有许多方法对原始数据举办调动可以使之stationary：
（1） 差分，即Integrated。 譬喻一阶差分是把原数列每一项减去前一项的值。二阶差分是一阶差分基本上再来一次差分。这是最推荐的做法
（2）先用某种函数大抵拟合原始数据，再用ARIMA处理惩罚剩余量。譬喻，先用一条直线拟合airline passenger的趋势，于是原始数据就酿成了每个数据点离这条直线的偏移。再用ARIMA去拟合这些偏移量。
（3）对原始数据取log可能开根号。这对variance不是常数的很有效。
#p#分页标题#e#
如何看数据是不是stationary呢？这里就要用到两个很常用的量了： ACF（auto correlation function）和PACF(patial auto correlation function)。对付non-stationary的数据，ACF图不会趋向于0，可能趋向0的速度很慢。 下面是三张ACF图，别离对应原始数据，一阶差分原始数据，去除周期性的一阶差分数据：
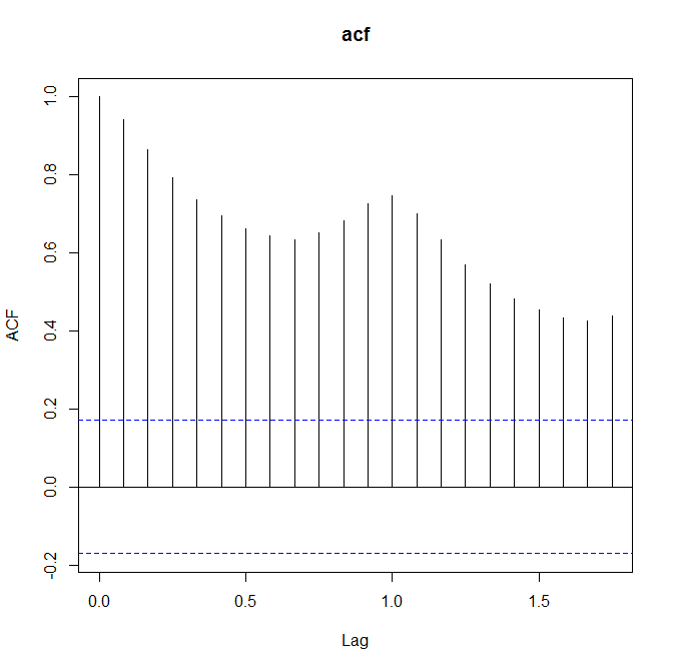
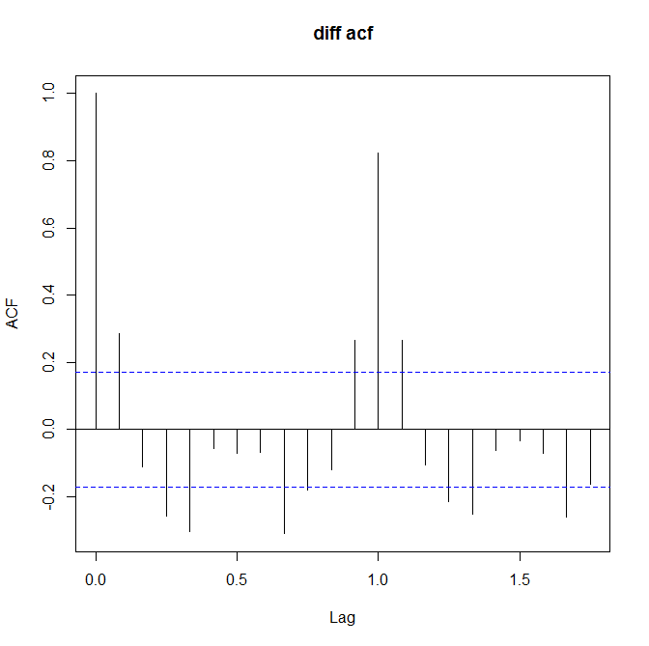
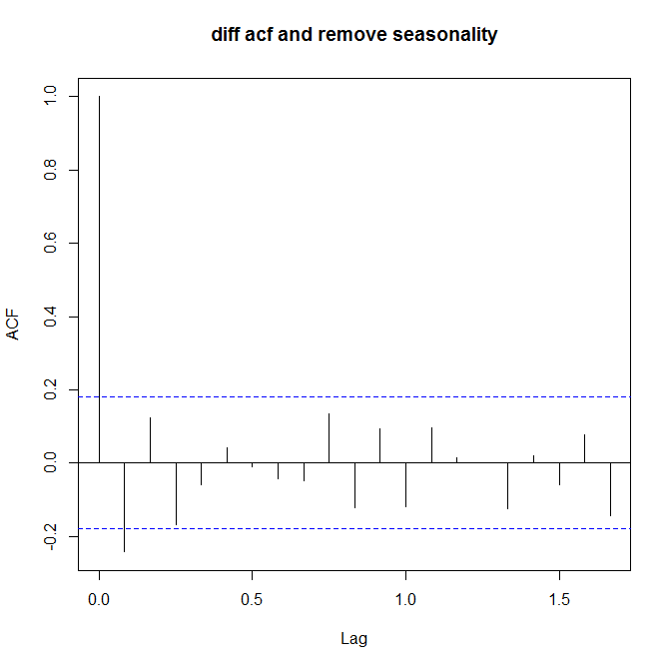
确保stationary之后，下面就要确定p和q的值了。定这两个值照旧要看ACF和PACF：
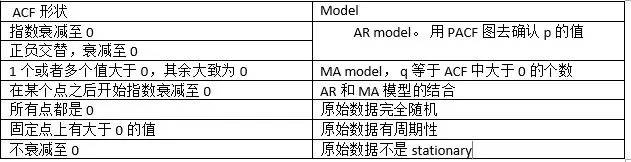
确定好p和q之后，就可以挪用R内里的arime函数了。 值得一提的是，R内里有两个很强大的函数： ets 和 auto.arima。 用户什么都不需要做，这两个函数会自动挑选一个最得当的算法去阐明数据。
在R中各个算法的结果如下：
代码如下：
passenger = read.csv(‘passenger.csv’,header=F,sep=’ ‘)
p<-unlist(passenger)
pt<-ts(p,frequency=12,start=2001)
plot(pt)
train<-window(pt,start=2001,end=2011+11/12)test<-window(pt,start=2012)
library(forecast)
pred_meanf<-meanf(train,h=12)
rmse(test,pred_meanf$mean) #226.2657pred_naive<-naive(train,h=12)
rmse(pred_naive$mean,test)#102.9765pred_snaive<-snaive(train,h=12)
rmse(pred_snaive$mean,test)#50.70832pred_rwf<-rwf(train,h=12, drift=T)
rmse(pred_rwf$mean,test)#92.66636pred_ses <- ses(train,h=12,initial=’simple’,alpha=0.2)
rmse(pred_ses$mean,test) #89.77035pred_holt<-holt(train,h=12,damped=F,initial=”simple”,beta=0.65)
rmse(pred_holt$mean,test)#76.86677 without beta=0.65 it would be 84.41239pred_hw<-hw(train,h=12,seasonal=’multiplicative’)
rmse(pred_hw$mean,test)#16.36156fit<-ets(train)
accuracy(predict(fit,12),test) #24.390252pred_stlf<-stlf(train)
rmse(pred_stlf$mean,test)#22.07215plot(stl(train,s.window=”periodic”)) #Seasonal Decomposition of Time Series by Loess
fit<-auto.arima(train)
accuracy(forecast(fit,h=12),test) #23.538735ma = arima(train, order = c(0, 1, 3), seasonal=list(order=c(0,1,3), period=12))
p<-predict(ma,12)
accuracy(p$pred,test) #18.55567BT = Box.test(ma$residuals, lag=30, type = “Ljung-Box”, fitdf=2)
