在R语言顶用自助法求统计量置信区间

当样本不切公道论漫衍假设时，求样本统计量的置信区间就成为一个困难。而自助法(Bootstrap)的思路是对原始样本反复抽样发生多个新样本，针对每个样本求取统计量，然后获得它的履历漫衍，再通过求履历漫衍的分位数来获得统计量的置信区间，这种要领不需要对统计量有任何理论漫衍的假设。一般认为，只要样本具有代表性，回收自助法需要的原始样本只要20-30个,反复抽样1000次就能到达满足的功效。

在R中举办自助法是操作boot扩展包，其流程如下：

编写一个求取统计量的自界说函数

将上面的函数放入boot（）函数中举办运算，获得自助法的功效

用boot.ci()函数求取置信区间

让我们用mtcars数据集来作为例子，我们可以将wt和disp作为自变量，mpg 作为因变量，举办回归后能获得一系列回归统计量。个中我们感乐趣的是鉴定系数R-square，但愿用自助法求它的95%置信区间。

首先界说求R-square的函数，留意个中的indices是必不行少的参数，别的一个参数代表样本数据
————————
rsq=function(data,indices){
d=data[indices,]
fit=lm(formula=mpg~wt+disp,data=d)
return(summary(fit)$r.square)
}
————————

载入boot扩展包，将随机种子设为1234，以利便获得沟通的功效，再操作boot函数获得功效results，个中R暗示反复抽样获得1000个样本
————————
library(boot)
set.seed(1234)
results=boot(data=mtcars,statistic=rsq,R=1000)
print(results)
plot(results)
————————



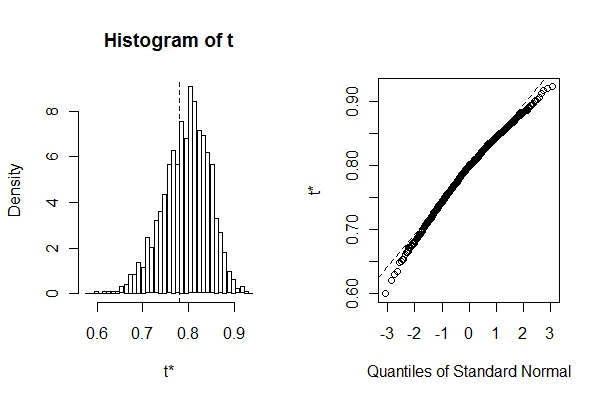
results这个数据布局中包罗了原始样本的统计量(results$t0)和再抽样样本的统计量(results$t0)，上图左侧的直方图暗示了再抽样样本的统计量的履历漫衍，个中的虚线暗示了原始样本的统计量，从中可以调查到毛病。右侧QQ图有助于判定履历漫衍是否正态。下面我们用boot.ci函数从功效中提取置信区间。

————————
boot.ci(results,conf=0.95,type=c(‘perc’,’bca’))
————————

个中conf暗示置信程度，type暗示了用何种算法来求区间，perc纵然用百分位要领，bca暗示adjusted bootstrap percentile，即对毛病举办了调解。功效如下：

BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS

Based on 1000 bootstrap replicates
CALL :

boot.ci(boot.out = results, conf = 0.95, type = c(“perc”, “bca”))
Intervals :

Level     Percentile            BCa

95%   ( 0.6838,  0.8833 )   ( 0.6344,  0.8549 )