利用neuralnet包在R中拟合一个神经网络模子
在我看来，神经网络老是浩瀚呆板进修模子傍边最让人感想欢快的个中一个模子。它不只因为含有一个成果强大的反向流传算法，并且这模子的巨大度（追念一下深度学校傍边许多的隐含层）和布局是来历于人脑布局。
然而，神经网络也并不老是很受接待，部门原因在于在某些环境下，它们的计较本钱很高，并且，与诸如感知向量机（SVMs）这样的简朴模子举办较量的时候，它们不见得能发生一个更好的功效。不外，我们再次谈起神经网络的时候，它照旧很风行的，也很容易引起人们的留意。
在这篇文章中，我们将要利用neuralnet包来建设神经网络模子，并建设一个线性回归模子来与此举办较量。
数据集我们将挪用MASS包来利用Boston数据集。Boston数据集就是关于Boston郊区的房价的数据集。我们的方针就是通过利用其它可行的持续变量来预测为小我私家所有的衡宇的房价的中位数。
set.seed(500)library(MASS)data <- Boston
首先，我们需要确认任何数据都不含有缺失值，而我们则要对此数据集举办必然的批改。apply(data,2,function(x) sum(is.na(x)))crim zn indus chas nox rm age dis rad tax ptratio 0 0 0 0 0 0 0 0 0 0 0 black lstat medv 0 0 0
很好，没发明任何缺失值。此刻，我们要把这个数据集，以随机的方法把它们分别为练习数据集和测试数据集，然后在此建设一个线性模子，并利用测试数据集举办测试。在这里，我们将利用glm()函数而不是lm()函数，那是因为后头我们要对线性模子举办交错检讨的时候，glm()函数会更有效。
index <- sample(1:nrow(data),round(0.75*nrow(data)))train <- data[index,]test <- data[-index,]lm.fit <- glm(medv~., data=train)summary(lm.fit)pr.lm <- predict(lm.fit,test)MSE.lm <- sum((pr.lm – test$medv)^2)/nrow(test)
Sample(x,size)函数简朴的输出了一个向量，它是从x向量傍边，基于一个特定的巨细随机选出来的一个模子。在默认环境下，抽样时我们无需对此举办转换：index就能很好浮现这个样本就是随机抽样了。
由于我们要处理惩罚线性回归模子，我们将要利用均值方差（MSE）作为一个指标来预测我们模子的拟合水平有几多。
对拟合一个神经网络模子做相应的筹备在拟合一个神经网络模子之前，我们需要做一些筹备事情。究竟，神经网络的练习和调试不是这么容易的。
第一步，我们需要对数据集举办预处理惩罚。在练习神经网络模子之前，对数据集举办准则化处理惩罚是一个不错的选择。我不想在这里强调这一步有何等的重要：基于你的数据集，假如没有对数据集举办准则化处理惩罚，这大概会导致一些对阐明毫无意义的功效的呈现，使得练习进程举办的很艰巨（大大都环境下，算法在达到较大答允迭代次数之前，是不会聚合的）。虽然，你可以利用差异的要领来阐明这个数据（z准则化、较大最小测试等等）。这里，我回收较大最小值得要领，并基于区间[0,1]来丈量数据。凡是来说，基于区间[0,1]或[-1,1]举办丈量好像能获得更好的功效。
因此，在举办下一步操纵之前，我们先丈量和疏散数据集：maxs <- apply(data, 2, max) mins <- apply(data, 2, min)scaled <- as.data.frame(scale(data, center = mins, scale = maxs – mins))train_ <- scaled[index,]test_ <- scaled[-index,]
记着，scale函数返回的功效是一个矩阵。因此，我们需要把它强制转换成数据框的名目。
参数我今朝所获悉的，就是今朝还没有一个的准则能让我们知道我们要用几多层和几多个神经元，就算今朝已经有一些被大部门人所接管的一些重要准则可以举办帮助也不能办理这样的问题。凡是来说，假如所有的都需要，一个隐含的层就可以举办大量利用了。一旦我们能确认神经元的数量，它该当处在输入层和输出层之间，凡是环境下，输入层占个中的2/3。最少，我那些短暂的举办一次又一次测试的经验好像是较好的谜底，因为我们无法担保这里的任何一条法则都能在较好的环境下切合你的模子。
因为这是一个用处不大的实例，我们将按照这个法则对两个层举办埋没。个中，输入层有13个输入值，两个埋没层别离有5个和3个神经元，而输出层，因为我们是做回归阐明，所以，只有一个输出值。
此刻，我们拟合一下这个网络：library(neuralnet)n <- names(train_)f <- as.formula(paste(“medv ~”, paste(n[!n %in% “medv”], collapse = ” + “)))nn <- neuralnet(f,data=train_,hidden=c(5,3),linear.output=T)
记着这么两点：1.基于某些原因，公式y~.不行以在neuralnet()函数傍边利用。首先，你必需要写一个完整的公式，并把它看成是一个参数用到拟合函数傍边。2.埋没的变量可以利用一个数值型向量来设定每个埋没层的神经元数目，而参数linear.output用于指定我们是否要举办回归阐明，此时，我们设定参数linear.output=TRUE，可能，分类，linear.output=FALSE。
nerualnet包提供了一个很好的作图东西：plot(nn)这是模子的图像，内里通过设定权重举办毗连：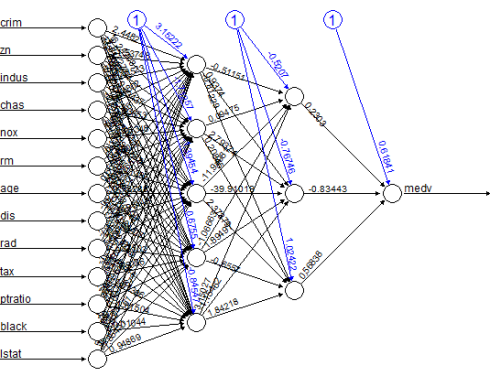
图中的黑线暗示每一层与其相关权重直接的干系，而蓝色线暗示拟合进程中，每一步被添加到蓝色线上的误差项。而这些误差可以暗示一个线性模子的误差区间。
这个网络本质上就是一个黑匣子。因此，对付它的拟合结果、权重和模子说太多。不外，我们可以确信，这个练习算法实现了聚合的结果。因此，我们可以利用这个模子举办阐明。
利用神经网络预测私有衡宇的价值此刻，我们可以对测试集里的值举办预测并计较它的均值方差（MSE）。记着，神经网络会输出一个准则化预测。所以，我们需要从头对它举办丈量和阐明，以便于做一些有意义的较量。
pr.nn <- compute(nn,test_[,1:13])pr.nn_ <- pr.nn$net.result*(max(data$medv)-min(data$medv))+min(data$medv)test.r <- (test_$medv)*(max(data$medv)-min(data$medv))+min(data$medv)MSE.nn <- sum((test.r – pr.nn_)^2)/nrow(test_)
此刻，我们较量它们俩的均值误差。print(paste(MSE.lm,MSE.nn))[1] “21.6297593507225 15.7518370200153″显然，在预测私人衡宇价值的时候，神经网络模子的机能优于线性模子。再次说明，我们任然要小心就是因为它的功效就是基于上面练习数据集分组时的机能。下面，做完图今后，我们会举办一个快速的交错检讨来使得功效更具有说服力。
基于测试数据集的神经网络和线性模子的第一步可视化操纵的图像如下：par(mfrow=c(1,2))plot(test$medv,pr.nn_,col=’red’,main=’Real vs predicted NN’,pch=18,cex=0.7)abline(0,1,lwd=2)legend(‘bottomright’,legend=’NN’,pch=18,col=’red’, bty=’n’)plot(test$medv,pr.lm,col=’blue’,main=’Real vs predicted lm’,pch=18, cex=0.7)abline(0,1,lwd=2)legend(‘bottomright’,legend=’LM’,pch=18,col=’blue’, bty=’n’, cex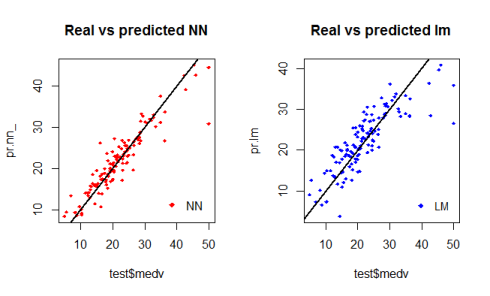
通过对其图像举办检讨，我们可以得知，由神经网络所作出的预测（一般环境下）要比那些线性模子所拟合出来的预测让散点越发接近拟合线（一条完美的准线，它暗示MSE为0。因此，这种预测的功效是抱负的）。plot(test$medv,pr.nn_,col=’red’,main=’Real vs predicted NN’,pch=18,cex=0.7)points(test$medv,pr.lm,col=’blue’,pch=18,cex=0.7)abline(0,1,lwd=2)legend(‘bottomright’,legend=c(‘NN’,’LM’),pch=18,col=c(‘red’,’blue’))也许，下面的这个图像所做出来的较量更有用。
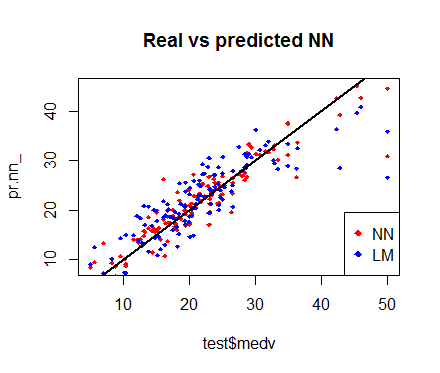（快速）交错检讨交错检讨是成立预测模子的另一个重要的步调。交错检讨的要领有好几种，其根基思想就是反复下面的进程屡次：
练习数据集疏散1.完成测试数据集疏散2.基于练习数据集拟合一个模子3.用测试数据集测试模子4.计较预测误差5.反复这个进程K次
然后，计较平均误差，它可以让我们获悉这个模子是奈何运作的。我们此刻要对神经网络利用for轮回语句来执行快速交错检讨，并利用boot包的cv.glm()函数来检讨线性模子。我今朝所知道的是，在R中，今朝还没有一个已经构建好的函数来对这种神经网络举办交错检讨。假如你知道R里有这种函数，请你在留言板哪里汇报我。下面，我们回收10次交错检讨的要领来验证线性模子的MSE：
library(boot)set.seed(200)lm.fit <- glm(medv~.,data=data)cv.glm(data,lm.fit,K=10)$delta[1] [1] 23.83560156对付这个网络，我们要知道我是这样疏散这些数据的：反复10次举办随机的90%的练习数据集和10%的测试数据集。并且，我也plyr包里初始化进度条，原因在于我想要存眷这个进程的执行环境，因为神经网络的拟合进程大概需要一点时间。set.seed(450)cv.error <- NULLk <- 10library(plyr) pbar <- create_progress_bar(‘text’)pbar$init(k)for(i in 1:k){ index <- sample(1:nrow(data),round(0.9*nrow(data))) train.cv <- scaled[index,] test.cv <- scaled[-index,] nn <- neuralnet(f,data=train.cv,hidden=c(5,2),linear.output=T) pr.nn <- compute(nn,test.cv[,1:13]) pr.nn <- pr.nn$net.result*(max(data$medv)-min(data$medv))+min(data$medv) test.cv.r <- (test.cv$medv)*(max(data$medv)-min(data$medv))+min(data$medv) cv.error[i] <- sum((test.cv.r – pr.nn)^2)/nrow(test.cv) pbar$step()}
拟合进程竣事今后，我们可以计较它的MSE均值并把功效举办可视化。mean(cv.error)10.32697995cv.error17.640652805 6.310575067 15.769518577 5.730130820 10.520947119 6.1211608406.389967211 8.004786424 17.369282494 9.412778105
作图代码如下：boxplot(cv.error,xlab=’MSE CV’,col=’cyan’, border=’blue’,names=’CV error (MSE)’, main=’CV error (MSE) for NN’,horizontal=TRUE)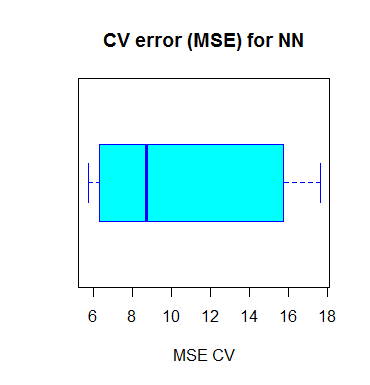
正如你在上图看到的那样，我们求出的这个神经网络的MSE均值为10.33，它比个中一个线性模子所算出来的功效要低，就算这里看起来像是交错检讨中，MSE的详细方差。这或者和数据集的解析方法有关，又可能是网络傍边权重的随机准则化有关。通过多次以差异的方法模仿这个进程，你可以获得一个更较准确的MSE预计值。
模子最终解读的启示神经网络和黑匣子有许多相似的处所，它对这些功效的解读比对一些诸如线性模子这样简朴模子的功效要难。因此，最终功效将取决于你是奈何用这个网络的，而你有大概用这样的原因举办表明。并且，正如你上面所看到的那样，我们还需要做一些特另外步调来拟合神经网络，而小小的变换可以引起功效上庞大的差异。
你可以在这里查阅这篇文章来看一下整段代码的方式地址。
接待插手本站果真乐趣群贸易智能与数据阐明群乐趣范畴包罗各类让数据发生代价的步伐，实际应用案例分享与接头，阐明东西，ETL东西，数据客栈，数据挖掘东西，报表系统等全方位常识QQ群：81035754
