函数预计

说到函数的预计我们可以必定的一点是我们很难获得原模子的函数，不外我们可以找到一个不坏的函数去迫近它，所以我们的函数预计从函数展开开始说起。

函数展开

Taylor展开

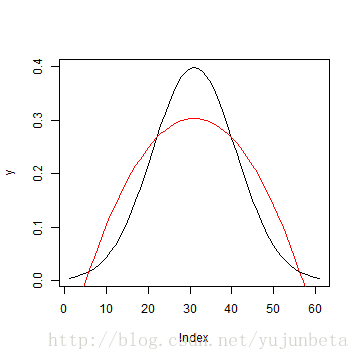
首先不得不提的就是台甫鼎鼎的Taylor展开，它汇报我们一个平滑的函数在x=t的一个邻域内有Taylor展式[ f(x)approxsum_{j=0}^{p}frac{f^{(j)}(t)}{j!}(x-t)^{j}=sum_{j=0}^{p}beta_{j}(x-t)^{j} ]它给我们的一个重要启示就是我们可以把我们感乐趣的函数拆解成若干个简朴函数( q_{0}(x),q_{1}(x)cdots, )的线性组合。[ f(x)=sum_{j=0}^{p}beta_{j}q_{j}(x) ]那么还剩一个问题，就是( q_{j}(x) )选什么。虽然一个简朴的选择就是( q_{j}(x)=x^{j} ),可能我们取( t=overline{x},q_{j}(x)=(x-overline{x})^{j} )。我们来看看这组函数基( q_{j}(x)=x^{j} )对尺度正态密度函数的预计结果：

x <- seq(-3, 3, by = 0.1)
y <- dnorm(x)
model <- lm(y ~ poly(x, 2))
plot(y, type = "l")
lines(fitted(model), col = 2)

summary(model)

## 
## Call:
## lm(formula = y ~ poly(x, 2))
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -0.07901 -0.06035 -0.00363  0.05864  0.10760 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.64e-01   8.09e-03    20.2   <2e-16 ***
## poly(x, 2)1 -1.77e-16   6.32e-02     0.0        1    
## poly(x, 2)2 -9.79e-01   6.32e-02   -15.5   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.0632 on 58 degrees of freedom
## Multiple R-squared:  0.805,  Adjusted R-squared:  0.799 
## F-statistic:  120 on 2 and 58 DF,  p-value: <2e-16

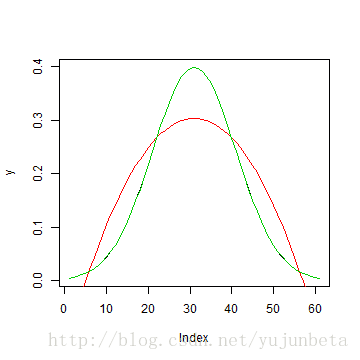
从图像上来看，这个拟合不是很好，我们可以认为是p较小造成的，一个办理步伐就是提高p的阶数，令p=10我们可以试试：

model1 <- lm(y ~ poly(x, 10))
x <- seq(-3, 3, by = 0.1)
y <- dnorm(x)
model <- lm(y ~ poly(x, 2))
plot(y, type = "l")
lines(fitted(model), col = 2)
lines(fitted(model1), col = 3)

summary(model1)

## 
## Call:
## lm(formula = y ~ poly(x, 10))
## 
## Residuals:
##       Min        1Q    Median        3Q       Max 
## -3.86e-04 -2.03e-04  1.45e-05  1.83e-04  2.83e-04 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    1.64e-01   2.94e-05  5572.4   <2e-16 ***
## poly(x, 10)1  -1.92e-16   2.29e-04     0.0        1    
## poly(x, 10)2  -9.79e-01   2.29e-04 -4268.8   <2e-16 ***
## poly(x, 10)3   2.36e-16   2.29e-04     0.0        1    
## poly(x, 10)4   4.54e-01   2.29e-04  1979.0   <2e-16 ***
## poly(x, 10)5  -1.65e-16   2.29e-04     0.0        1    
## poly(x, 10)6  -1.54e-01   2.29e-04  -672.4   <2e-16 ***
## poly(x, 10)7   1.67e-17   2.29e-04     0.0        1    
## poly(x, 10)8   4.09e-02   2.29e-04   178.5   <2e-16 ***
## poly(x, 10)9   2.07e-16   2.29e-04     0.0        1    
## poly(x, 10)10 -8.85e-03   2.29e-04   -38.6   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.000229 on 50 degrees of freedom
## Multiple R-squared:     1,   Adjusted R-squared:     1 
## F-statistic: 2.26e+06 on 10 and 50 DF,  p-value: <2e-16

从上图看到，拟合结果好了不少，这样看上去我们只需要提高基函数阶数就可以办理拟合优度的问题了。可是留意到跟着阶数提高，大概呈现设计阵降秩的景象，也有大概呈现复共线性，这是我们不但愿看到的。为了办理第一个问题，我们的做法是限制p的较大取值，如将p限制在5以下；对付第二个问题，我们的做法即是回收正交多项式基。

正交多项式展开

正交多项式的相关界说可以参阅wiki，这里就不在烦琐了，我们这里列出Legendre多项式基与Hermite多项式基。
个中Legendre多项式基已经在wiki中给出了，其取值范畴是[-1,1]，权函数是1，表达式为：[ p_{0}(t)=1,p_{1}(t)=tp_{2}(t)=(3t^2-1)/2,p_{3}=(5t^3-3t)/2 ]Legendre多项式基的递归表达式可以表达为：[ p_{k}(t)=frac{2k-1}{k}tp_{k-1}(t)-frac{k-1}{k}p_{k-2}(t) ]

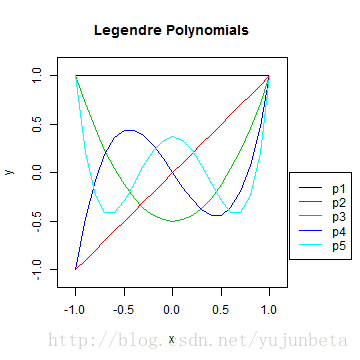
Hermite多项式基的取值范畴为( (-infty,infty) ),对应的权函数是尺度正态漫衍的核函数，表达式为：[ H_{0}^{e}(t)=1,H_{1}^{e}(t)=tH_{2}^{e}(t)=t^2-1,H_{3}^{e}(t)=t^3-3tH_{4}^{e}(t)=t^4-6t^2-3,H_{5}^{e}=t^5-10t^3+15t ]Hermite多项式基的递归表达式可以表达为:[ H_{k}^{e}(t)=tH_{k-1}^{e}(t)-(k-1)H_{k-2}^{e}(t) ]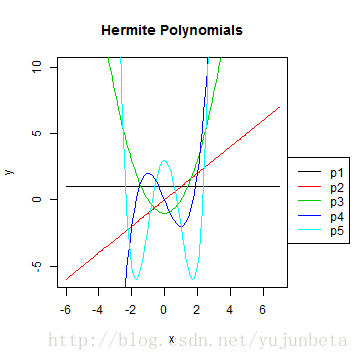

#p#分页标题#e#

我们这里来看一个例子，假设真实模子为( y=5xcos(5pi x) ),我们一共做了10次试验，获得了10个视察，此刻我们要找一个拟模子来近似这个真实模子。我们来看看多项式基的结果：

x <- seq(-1, 1, length = 20)
y <- 5 * x * cos(5 * pi * x)
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1)
points(x, y)
A <- data.frame(x = seq(-1, 1, length = 1000))
model.linear <- lm(y ~ poly(x, 6))
lines(seq(-1, 1, length = 1000), predict(model.linear, A), col = 2)
model.linear1 <- lm(y ~ poly(x, 9))
lines(seq(-1, 1, length = 1000), predict(model.linear1, A), col = 3)
z <- matrix(rep(NA, 6 * length(x)), length(x), 6)
z[, 1] <- x
z[, 2] <- (3 * x^2 - 1)/2
z[, 3] <- (5 * x^3 - 3 * x)/2
z[, 4] <- (35 * x^4 - 30 * x^2 + 3)/8
z[, 5] <- (2 * 5 - 1)/5 * x * z[, 4] - 0.8 * z[, 3]
z[, 6] <- (2 * 6 - 1)/6 * x * z[, 5] - 5/6 * z[, 4]
model.linear2 <- lm(y ~ z)
x <- seq(-1, 1, len = 1000)
z <- matrix(rep(NA, 6 * length(x)), length(x), 6)
z[, 1] <- x
z[, 2] <- (3 * x^2 - 1)/2
z[, 3] <- (5 * x^3 - 3 * x)/2
z[, 4] <- (35 * x^4 - 30 * x^2 + 3)/8
z[, 5] <- (2 * 5 - 1)/5 * x * z[, 4] - 0.8 * z[, 3]
z[, 6] <- (2 * 6 - 1)/6 * x * z[, 5] - 5/6 * z[, 4]
B <- as.data.frame(z)
lines(x, predict(model.linear2, B), col = 4)
letters <- c("orignal model", "6 order poly-reg", "9 order poly-reg", "6 order orth-reg")
legend("bottomright", legend = letters, lty = 1, col = 1:4, cex = 0.5)

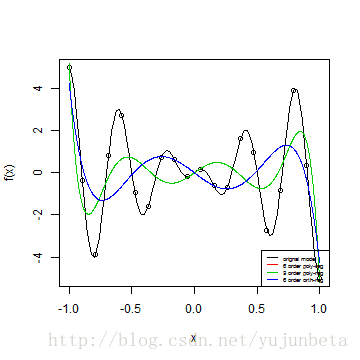
Fourier展开

这里我们就可以看到，多项式拟合对付这种含周期的问题的办理结果是很欠好的，正交多项式完全不可，可见问题并不是出在复共线性上，对付含周期的函数的迫近我们可以引入Fourier基：[ 1,cos(2pi x),sin(2pi x),cdots,cos(2ppi x),sin(2ppi x),cdots ]我们来看看拟合结果：

x <- seq(-1, 1, length = 10)
y <- 5 * x * cos(5 * pi * x)
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1, ylim = c(-15.5, 15.5))
points(x, y)
model.linear <- lm(y ~ poly(x, 7))
A <- data.frame(x = seq(-1, 1, length = 1000))
lines(seq(-1, 1, len = 1000), predict(model.linear, A), col = 2)
model.linear1 <- lm(y ~ poly(x, 9))
lines(seq(-1, 1, len = 1000), predict(model.linear1, A), col = 3)
z <- matrix(rep(NA, 6 * length(x)), length(x), 6)
z[, 1] <- cos(2 * pi * x)
z[, 2] <- sin(2 * pi * x)
z[, 3] <- cos(4 * pi * x)
z[, 4] <- sin(4 * pi * x)
z[, 5] <- cos(6 * pi * x)
z[, 6] <- sin(6 * pi * x)
model.linear2 <- lm(y ~ z)
x <- seq(-1, 1, len = 1000)
z <- matrix(rep(NA, 6 * length(x)), length(x), 6)
z[, 1] <- cos(2 * pi * x)
z[, 2] <- sin(2 * pi * x)
z[, 3] <- cos(4 * pi * x)
z[, 4] <- sin(4 * pi * x)
z[, 5] <- cos(6 * pi * x)
z[, 6] <- sin(6 * pi * x)
B <- as.data.frame(z)
lines(x, predict(model.linear2, B), col = 4)
letters <- c("orignal model", "7 order poly-reg", "9 order poly-reg", "Fourier-reg")
legend("bottomright", legend = letters, lty = 1, col = 1:4, cex = 0.5)

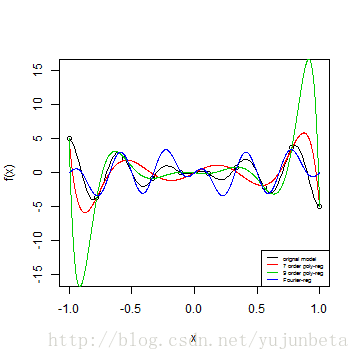
可见Fourier基对周期函数的拟合照旧很好的。可是这必需是不含趋势的功效，含趋势的只能在局部有个不错的拟合，假如我们把上面的模子换为( 5x+cos(5pi x) ),可以看到Fourier基拟合的结果是十分糟糕的。

x <- seq(-1, 1, length = 10)
y <- 5 * x + cos(5 * pi * x)
f <- function(x) 5 * x + cos(5 * pi * x)
curve(f, -1, 1)
points(x, y)
model.linear <- lm(y ~ poly(x, 7))
A <- data.frame(x = seq(-1, 1, length = 1000))
lines(seq(-1, 1, len = 1000), predict(model.linear, A), col = 2)
model.linear1 <- lm(y ~ poly(x, 9))
lines(seq(-1, 1, len = 1000), predict(model.linear1, A), col = 3)
z <- matrix(rep(NA, 6 * length(x)), length(x), 6)
z[, 1] <- cos(2 * pi * x)
z[, 2] <- sin(2 * pi * x)
z[, 3] <- cos(4 * pi * x)
z[, 4] <- sin(4 * pi * x)
z[, 5] <- cos(6 * pi * x)
z[, 6] <- sin(6 * pi * x)
model.linear2 <- lm(y ~ z)
x <- seq(-1, 1, len = 1000)
z <- matrix(rep(NA, 6 * length(x)), length(x), 6)
z[, 1] <- cos(2 * pi * x)
z[, 2] <- sin(2 * pi * x)
z[, 3] <- cos(4 * pi * x)
z[, 4] <- sin(4 * pi * x)
z[, 5] <- cos(6 * pi * x)
z[, 6] <- sin(6 * pi * x)
B <- as.data.frame(z)
lines(x, predict(model.linear2, B), col = 4)
letters <- c("orignal model", "7 order poly-reg", "9 order poly-reg", "Fourier-reg")
legend("bottomright", legend = letters, lty = 1, col = 1:4, cex = 0.5)

#p#分页标题#e#

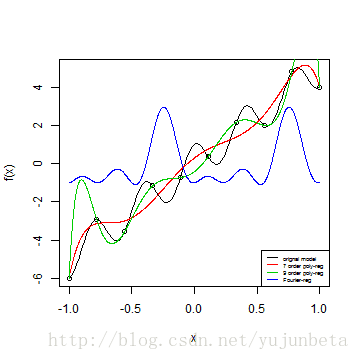
样条基展开

有些时候我们对全局的拟合是有缺陷的，所以可以举办分段的拟合，一旦确定了分段的临界点，我们就可以举办局部的回归，样条根基上就警惕了这样一个思想。
为了增加局部的拟合优度，我们在本来的函数基( 1,x,x^2,cdots,x^p )上加上( (x-knot_i)_+^p,(i=1,2,…) )个中，knot暗示节点，函数( (x-knot_i)_+ )暗示函数( (x-knot_i) )取值为正时取函数值，不然取0.

x <- seq(-1, 1, length = 20)
y <- 5 * x * cos(5 * pi * x)
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1)
points(x, y)
model.reg <- lm(y ~ poly(x, 5))
A <- data.frame(x = seq(-1, 1, length = 1000))
lines(seq(-1, 1, len = 1000), predict(model.reg, A), col = 2)
ndat <- length(x)
knots <- seq(-1, 1, length = 10)
f <- function(x, y) ifelse(y > x, (y - x)^3, 0)
X <- matrix(rep(NA, length(x) * (3 + length(knots))), length(x), (3 + length(knots)))
for (i in 1:3) X[, i] <- x^i
for (i in 4:(length(knots) + 3)) X[, i] <- f(knots[(i - 3)], x)
model.cubic <- lm(y ~ X)
x <- seq(-1, 1, length = 1000)
X <- matrix(rep(NA, length(x) * (3 + length(knots))), length(x), (3 + length(knots)))
for (i in 1:3) X[, i] <- x^i
for (i in 4:(length(knots) + 3)) X[, i] <- f(knots[(i - 3)], x)
A <- as.data.frame(X)
lines(seq(-1, 1, len = 1000), predict(model.cubic, A), col = 3)

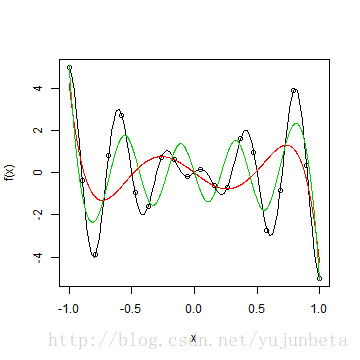
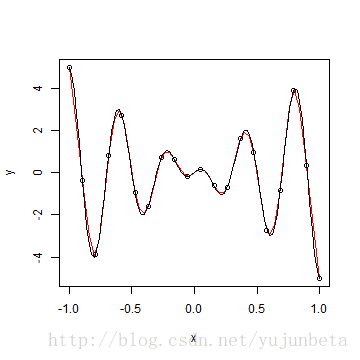
从上图中我们可以看到加上样条基后，拟合结果瞬间提高了不少，三阶样条基就可以对抗5~6阶的多项式基了。R中的splines包中提供了polyspline函数，来做样条拟合，我们可以看看在这个例子中它险些就是原函数的“复制”。

x <- seq(-1, 1, length = 20)
y <- 5 * x * cos(5 * pi * x)
library(splines)
model <- polySpline(interpSpline(y ~ x))
# print(model)
plot(model, col = 2)
f <- function(x) 5 * x * cos(5 * pi * x)
curve(f, -1, 1, ylim = c(-15.5, 15.5), add = T)
points(x, y)

本节的最后，我们最厥后看看函数展开的相关内容，假如说我们已经知道了函数( f(x) )的表达式，想求解一个近似的函数展开式的系数，我们只需要将( f(x) )拆解为( f(x)=g(x)p(x) ),个中( p(x) )为密度函数，那么展开式系数可以近似的暗示为( hat c_k=frac{1}{n}sum_{i=1}^{n}q_k(x_i)g(x_i) )个中( x_1,cdots,x_n )是由( p(x) )发生的随机数。

本作品回收常识共享署名-非贸易性利用-沟通方法共享 4.0 国际许可协议举办许可。