用R语言举办分位数回归：基本篇第五节

分位数回归的图形功效

# 绘图# 参数较量windows(5,5)plot(s1)windows(5,5)plot(s2)windows(5,5)plot(s3) # 散点图# – 总体windows(5,5)attach(dat2)plot(lnincome,lnfoodexp,cex=0.25,type=”n”, xlab=”Personal Income”, ylab=”Food Expenditure”, main=”Income and Food Expenditure”)points(lnincome,lnfoodexp,pch=”.”,col=”blue”)abline( rq(lnfoodexp ~ lnincome, tau=0.5, method=”fn”), col=”blue” )abline( lm(lnfoodexp ~ lnincome), lty = 2, col=”red” )taus = c(0.05, 0.1, 0.25, 0.75, 0.9, 0.95)for(i in 1:length(taus)){ abline( rq(lnfoodexp ~ lnincome, tau=taus[i], method=”fn”), col=”gray” )}legend(“bottomright”,c(“QR”,”OLS”),col=c(“blue”,”red”),lty=1:2,bty=”n”)detach(dat2)# – 城镇windows(5,5)dat2a = dat2[dat2$urtype==1,]attach(dat2a)plot(lnincome,lnfoodexp,cex=0.25,type=”n”, xlab=”Personal Income”, ylab=”Food Expenditure”, main=”Income and Food Expenditure”)points(lnincome,lnfoodexp,pch=”.”,col=”blue”)abline( rq(lnfoodexp ~ lnincome, tau=0.5, method=”fn”), col=”blue” )abline( lm(lnfoodexp ~ lnincome), lty = 2, col=”red” )taus = c(0.05, 0.1, 0.25, 0.75, 0.9, 0.95)for(i in 1:length(taus)){ abline( rq(lnfoodexp ~ lnincome, tau=taus[i], method=”fn”), col=”gray” )}legend(“bottomright”,c(“QR”,”OLS”),col=c(“blue”,”red”),lty=1:2,bty=”n”)detach(dat2a)# – 农村windows(5,5)dat2b = dat2[dat2$urtype==2,]attach(dat2b)plot(lnincome,lnfoodexp,cex=0.25,type=”n”, xlab=”Personal Income”, ylab=”Food Expenditure”, main=”Income and Food Expenditure”)points(lnincome,lnfoodexp,pch=”.”,col=”blue”)abline( rq(lnfoodexp ~ lnincome, tau=0.5, method=”fn”), col=”blue” )abline( lm(lnfoodexp ~ lnincome), lty = 2, col=”red” )taus = c(0.05, 0.1, 0.25, 0.75, 0.9, 0.95)for(i in 1:length(taus)){ abline( rq(lnfoodexp ~ lnincome, tau=taus[i], method=”fn”), col=”gray” )}legend(“bottomright”,c(“QR”,”OLS”),col=c(“blue”,”red”),lty=1:2,bty=”n”)detach(dat2b)

功效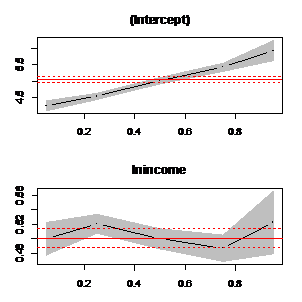：用R语言举行分位数回归：根基篇第五节图3.2.a 整体数据的分位数回归的系数走势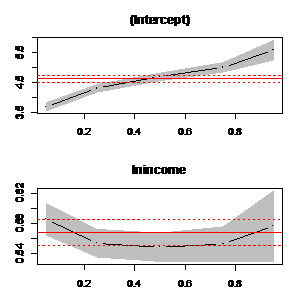图3.2.b 城镇数据的分位数回归的系数走势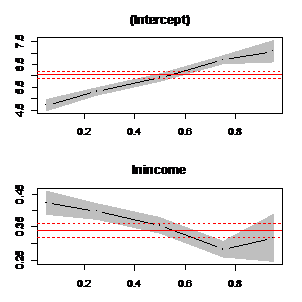图3.2.c 农村数据的分位数回归的系数走势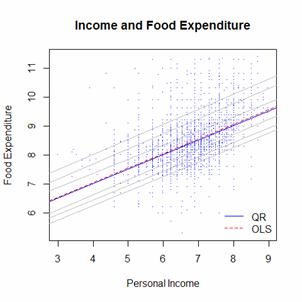图3.3.a 全部数据的分位数回归的散点图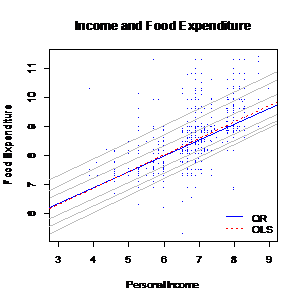图3.3.b 城镇数据的分位数回归的散点图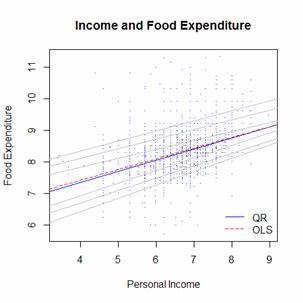用R语言举行分位数回归：根基篇第五节图3.3.c 农村数据的分位数回归的散点图（六）分位数解析

凭据MM2005要领举办解析。留意的是：

1、group参数必需是包括1和2的向量，个中反事实模子的拟合值是回收1类的模子参数和2类的数据计较获得。相应地，在本案例中作为参照的拟合功效是假定农村流感人口凭据城镇的抉择模子，会获得什么样的食品支出。

2、data参数中只能包括模子中呈现的变量。好比这里利用的变量只包罗lnfoodexp和lnincome，所以只能保存这两个变量在data中。

# 凭据城乡举办解析group = as.character( dat2$urtype ) # 必需担保group是包括1和2的向量group[group==”1″] = 1group[group==”2″] = 2taus = c(0.05,0.25,0.5,0.75,0.95)data = dat2[,c(“lnfoodexp”,”lnincome”)]res = MM2005(lnfoodexp ~ lnincome,taus, data, group, pic=F, m.rq=”fn”)# 分位数总差别回报影响变量影响# 0.05 -0.051089859 0.06520406 -0.11629392# 0.25 -0.056506090 0.04647729 -0.10298338# 0.50 -0.014632774 0.08108505 -0.09571782# 0.75 0.009629691 0.10826533 -0.09863564# 0.95 0.028791246 0.10291667 -0.07412543write.csv(res,”tab-MM2005.csv”,row.names=F) # 将功效生存为csv表格，利便整理

功效：表3-2 分位数解析：按城乡的解析

分位数	总差别	回报影响	变量影响
0.05	-0.22	-0.04	-0.18
0.25	-0.18	-0.01	-0.17
0.50	-0.23	-0.06	-0.17
0.75	-0.27	-0.10	-0.17
0.95	-0.41	-0.23	-0.17

以上功效显示，无论对付高收入家庭照旧低收入家庭，个别对食品支出的影响都差不多。但对付高收入家庭（分位数较高），总差别和回报影响更大。说明城乡高收入人群的食品消费差别较大，个中主要的差别来自于斜率的差异，即食品消费关于收入的敏感性差异带来的差别。

当前位置：以往代写 > 其他教程 >用R语言举办分位数回归：基本篇第五节