在C/C++算法设计中利用任意位宽

副标题#e#

开拓定点(fixed-point)算法时，凡是需要在设计成果性、数字精度建模、及验证(仿真)速度之间取得一个均衡。此刻，一种新的数据类可使此进程简朴化，由此获得更简朴准确的建模精度、更好的数字求精、及更快的验证周期，而ANSI C/C++正是开拓这种数字求精算法的最佳语言。

某此算法天生就合用于操纵整数，或那些抱负中的实数(如数字滤波器的系数)，它们也大概会利用浮点或定点范例。一般而言，在算法开拓的早期阶段，会常常用到C语言的float或double浮点范例，因为它们可提供一个很是大的动态数据范畴，且对大大都措施来说都是合用的。见图1：

利用C内置的float范例来建模一个FIR滤波器

算法可举办数字求精，以便利用定点算术来低落最终硬件或软件实现的巨大性。在硬件方面，将整数或定点算术限制为最小位宽，可在本质上满意机能、空间、能耗的需要;假如实现顶用到了DSP处理惩罚器，那么把算法限制为整数或定点算术，就可为特定措施利用尽大概自制的处理惩罚器。

定点算术的建模可通过C语言内置的浮点或整数范例来完成，这做的话，需要显式编码并受限于C中浮点数及整数可暗示的最大数：64位整数或53位尾数;这些城市给操纵数的位宽带来更多的限制，譬喻，2个33位的数相乘，会高出64位C整数可暗示的范畴。图2演示了一个FIR滤波器的例子，但temp变量限制为15位的定点精度，个中10位用于整数位。在这个实现中，LSB的右部位被舍弃(量化模子的截断)，而MSB的左部位也被舍弃(包装的溢出模子)，应该意识到，利用float(或double)的模子在精度上是受限的，且不能再次合成(synthesis)。同样，由于有取整模子的严格位精度界说有先，又由于内置浮点范例的取整将会先被应用，所以对除法这样的操纵来说，就很是难实现了。

利用float建模定点行为

当很多算法都能依赖当地C数据范例的精度来编写时，对支持任意长度的整数及定点算法，各人就会抱有极大的期望，而硬件描写语言(HDL)如VHDL，走的也是同一条路。跟着C/C++越来越多地被用于高级合成与验证东西(High-Level Synthesis and Verification tools)，也证明白这种语言本质上有一个足以满意当前及将来措施需要的数据范例库。任意长度范例的支持，也可使数据范例的行为有一个统一的界说，而统一的语义则制止了人工实现上的一些限制。

算法C数据范例

算法C数据范例是一种基于类的C++库，其实现了任意长度的整数及定点范例，而这些可自由会见的范例有一系列长处，包罗统一及精采界说的语义，尚有媲美C/C++内置数据范例的运行时速度，比拟SystemC中相应的范例，其运行速度也高出10倍以上。这些数据范例能用于任何切合C++或SystemC类型尺度的措施中，并拥有高度可合成的语义。

语义

语义的统一性与一致性是制止在算法中，产生成果性错误的要害，以下的例子，也说明白这点：

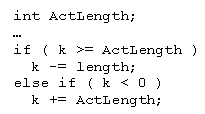
#p#副标题#e#

众所周知，变量ActLength的范畴为1至255，万一编译器的合成不知道其范畴，就不能举办相应的优化，它的声明就会从int变为更严格的sc_uint<8>范例;固然合成会获得更好的功效，但设计就仿真得不正确了。在颠末一番调试之后，找到了问题的源头：在较量表达式k >= ActLength中，两个操纵数酿成了一个signed int与一个unsigned long long(为64位无标记整数，其是sc_uint范例的基范例)之间的较量。对此的表明是：C/C++整数晋升法则指定了在举办较量之前，会把操纵数int晋升为一个unsigned long long，譬喻，假如k的值为 -1，在晋升为unsigned long long之后，它会酿成2^64 – 1。

像这样语义中的问题一般会很是难以察觉，且是与位宽相关的，譬喻，大概有人想扩大某个现有算法的位宽，只有看到功效时，才知道是行不通的;这个问题也大概是与特定平台相关的，譬喻，对1 << 32(两个操纵数都是int范例，功效也是int范例)各人期望返回0，但在大大都平台(或编译器)上，它城市返回1(没有移位，只因为第二个操纵数较低的五位被计较进来了);当第一个操纵数是一个64位整数时，平台依赖性会表示得越发明明及频繁。主要的问题是C/C++尺度没有指定在32位整数环境下移位值(第二个操纵数)超出0至31范畴、或在64位整数环境下移位值超出0至63范畴时的行为。不幸的是，像sc_int、sc_uint这样的数据范例也不能为用户制止这类平台依赖性的问题。

#p#分页标题#e#

算法C数据范例被设计用于提供统一且一致的语义，因此，它们是可预测的，譬喻，对有标记数混用一个无标记操纵数仍会发生期望的功效;这些范例的长度不受限制，所以就不存在所谓的精度问题。所有的操纵——包罗移位和除法——都有完整且一致性的界说，殽杂差异的范例也能获得期望的功效，如，当x为一个C内置范例，而y是一个算法C范例时，表达式x+y和y+x均能返回沟通的功效。

运行时间

我们的目标是为了在支持任意长度范例及制止用户遇到前述语义问题的前提下，获得利用内置范例(位宽不高出64位)手工C/C++编码优化过的运行时间。算法C范例是为快速执行及易于合成的语义而设计及实现的，所有操纵的位宽由C++编译器静态确定，这就制止了动态内存分派，淘汰了运行时间，也使得语义越发易于合成。别的，实现也为速度举办了优化，因此大概会挪用更多的专用及高效代码，充实操作了当今编译器的优化特性。

表1：规格化为ac_fixed的运行时间较量

表1是当定点算术用算法C定点范例ac_fixed来建模时，各类差异的运行时较量;float的实此刻图2中，sc_fixed_fast为SystemC中精度受限的定点数据范例，sc_fixed为任意精度的定点范例。实际中对FIR滤波器举办10^8次挪用，TRN/WRAP的运行时间为6.5秒，RND/SAT为29秒。其他范例的运行时间也能从这张表中依次推出，如sc_fixed TRN/WRAP将耗费6.5s × 227 = 1476s(快要25分钟)。作为参考，图1中的算法(利用无定点建模的float)耗费时间为3.5s(比起利用定点建模的ac_fixed，慢了近两倍)。

上述的运行时间数据，均由GCC 4.1.1丈量得来，而在之前版本的GCC或Visual C++ 2005中获得的数据大抵靠近。

别的，运行时间也能通过整型数据范例或位操纵进一步缩短。表2为一个DCT算法的相应功效，它由一个每次读写2位的移位操纵得来，与此比拟的运行时间为SystemC精度受限的sc_int与任意长度的sc_bigint。

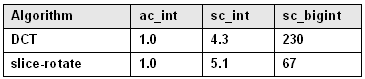
表2：规格化为ac_int的运行时间较量

结论

基于通用尺度ANSI C++，这种新的整数与定点算法C范例答允算法及系统设计者指定任意位宽，从而提供比传统数据范例高200倍的仿真效率。这些新数据范例可成为C-to-RTL设计链中很是有代价的一环，及在整个实现流程中担保了任意位宽的精度。