简朴二叉树类
当前位置：以往代写 > C/C++ 教程 >简朴二叉树类

简朴二叉树类

2019-06-13

简朴二叉树类

简朴二叉树类

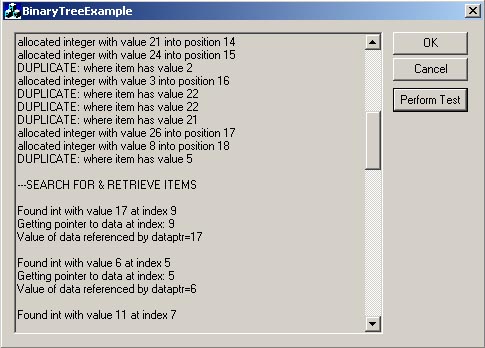
副标题#e#简单二叉树类

本文由DigitalConvict供稿。

原文出处：http://www.codeguru.com/algorithms/SimpleBinaryTree.html

情况: (无出格限制) 在VC6 上开拓

我不会具体先容二叉树理论的具体细节，因为这些对象，Per Nilsson 已经在他的“二叉树”中接头过了，你可以在如下地点here找到具体的细节。

对半查找树对付找到在一个列表中很少变革的项来说是很有用的。添加和删除操纵的开销是很大的，只主要是因为对半查找树的均衡性所抉择的。

我们可以这样说这个类是在同一主题上的一个差异的执行方法。

执行细节

建设这棵树

要建设二叉树，可以简朴的建设一个CSimpleBinaryTree 工具并初始化。

#define MAXELEMS 100
CSimpleBinaryTree btree;
btree.Initialise(MAXELEMS,sizeof(CSomeObject));或btree.Initialise(MAXELEMS,sizeof(CSomeObject), someCompareFunction);或btree.Initialise(MAXELEMS,sizeof(CSomeObject), someCompareFunction, nGrowTrigger, nGrowByValue, nShrinkTrigger, nShrinkByValue);"someCompareFunction"是一个有两个指针参数的函数的指针，这个函数按照第一个参数是否小于，便是，大于第二个参数而别离返回负数，0和正数。CSimpleBinaryTree 提供了一个通用的全局较量函数，它可以较量两个长整型的指针。


#p#副标题#e#

添加元素

要向这棵树添加一个子项,可以简朴的挪用AddItem()并传一个指针给它，用来存放添加后的工具。在内部，相关数据通过指针被拷贝到动态分贝的内存上。CSomeObject sObj;
CSomeObject *psObj1=&sObj;
CSomeObject psObj2;
int nResult;
nResult=btree.AddItem(&sObj);或nResult=btree.AddItem(psObj1);或nResult=btree.AddItem(psObj1, psObj2);AddItem() 函数返回两个值。第一个是整型功效。假如子项被乐成添加了，子项的索引值会被乐成返回，假如没有乐成添加，就会返回错误代码:

· DUPLICATE_FOUND

· OUT_OF_MEMORY

· TREE_IS_FULL

第二个返回值是可选择的第二个参数值。假如操纵乐成,那末指向新建设工具的指针被返回了, 假如操纵不乐成，该指针被赋值为空。

DUPLICATE_FOUND仅当民众变量m_bAllowDuplicates被设为FALSE时才返回，不然，这个树将答允复制数据（缺省环境）。

假如复制操纵不被答允，那末这棵树将会在每次被搜索时城市添加子元素以便判定子元素是否存在。这一点就低落了添加子项的速度，可是也潜在的节减了内存分派的数量。

删除元素

要删除一个子项，可以简朴的挪用RemoveItem() 函数，并配置上我们要删除的子项的索引值。

BOOL bResult;
bResult=RemoveItem(nIndex);

假如该项被乐成地从树中删除了,函数返回TRUE, 不然返回FALSE;

当一个子项从树中删除时，其上面所有的元素对应的子项左移一个位置并“子项总数”减一。

这一点，说明效率并不高,潜在的,函数有大概不得不遍历整棵树.无论如何从二叉树添加和删除元素是天生的比其他的存储/修补算法要慢，这是因为二叉遍历网络树要求元素有序的事实。

遍历这棵树

要判定一个元素是否在这棵树中存在,可以简朴的挪用FindItem() 函数.int nIndex;
nIndex = btree.FindItem(psObj);或CSomeObject *pFoundObject;
nIndex = btree.FindItem(psObj,pFoundObject);FindItem() 返回两个值.假如子项存在，第一个值就是子项的索引值，假如不存在，赋值为ITEM_NOT_PRESENT value.第二个返回值是可选择的第二个参数值。假如子项被发明白，pFoundObject 将指向它在树中的工具,假如子项没有被发明，pFoundObject 赋为空;

在CSimpleBinaryTree 中有两个搜索算法.线性搜索和对半搜索.线性搜索只在树种子项数目小于指定值的时候才利用 (缺省为10),从这个点今后的各项，将利用对半搜索.这样做的原因是线性查找不要求元素举办排序而且它的运算法则相对要简朴的多.因此对付小数目项来说，线性查找是抱负的.

假如在树中答允复制(m_bAllowDuplicates=TRUE) ，那末均衡(所有子项排序)操纵只有当在“被要求”的时候举办，而不是像m_bAllowDuplicates=FALSE and而且所有子项在每次添加新的子项时城市举办排序.相反地,排序大概会在挪用FindItem() 函数时举办.当用FindItem()查找一个子项时，利用的是对半查找算法,纵然该项存在，查找也大概失败.这样的原因是这个树并不是完全均衡的.这这种环境下，算法查找子项时，就会失败,同时也说明该树并非完全均衡的,通过排序使得该树均衡，然后再递归的挪用FindItem()函数.一旦该树均衡了，一个内部标志将会被配置，而且这个标志在添加一个新元素时不会被配置,因而制止了任何一个递归的轮回.因从此来的FindItem()挪用就会制止反复的挪用.对付措施员来说，没有须要作些非凡的操纵.以上说的只是这个类中浩瀚内部处理惩罚中一个罢了.

#p#分页标题#e#

这样在答允复制操纵的时候，每添加一个子项就不必再挪用SortItems() 了，从而效率获得很大的提高.此处利用的是C 语言库中的qsort()函数来实现排序算法的.

重设树的巨细

通过ReSize()来配置二叉树的子项数目，以满意添加和删除的需要.btree.ReSize(300);通过挪用ReSize()可以配置树中可以容纳的最大子项数. 然而当树中已经存在200个元素而且其最大容纳子项数为250， 假如作如下挪用btree.ReSize(100),那末树中开始的100元素 将会传送到新的指针数组上面，尔后头的120个元素将会从树中被移除，其占用的内存也会被释放掉.

通过配置民众成员变量m_bAutoResize = TRUE (缺省),该树可以通过成员变量顶用于节制增减和淘汰的参数自动的配置元素数目标巨细.

#p#副标题#e#

增加和消减

当民众成员变量m_bAutoResize被设为TRUE时，增加和消减参数节制树的元素数目.每项操纵会有两个变量.一个触发器，一个增加/消减值.所有的值用占当前树中元素数目标百分比来暗示.

触发器的值可以确定增长或消减操纵的产生.增加/消减 的百分比确定了该树增加或消减的水平.

好比，假如在树中我有80 元素，被答允的最大子项数为100，m_bAutoResize 设为TRUE.同样的增长触发器被设为90 (90%) ，消减触发器被设为10 (10%)，增长和消减的值都设为50 (50%).

假如我向树中添加11个元素,该树将会有91%的填充率，同时增长触发器也会被激活.那末此时该树可容纳的元素数目就会增加50%,i.e. 在内部会挪用ReSize(150).同样的，假如我删除了80 个元素中的71个，该树将只有9%的填充率，消减触发器会被激活，从而导致树中可容纳元素树消减50%,i.e. 在内部会挪用ReSize(50).

重设巨细的操纵价钱昂贵，因此应该尽大概的制止.上面的例子中给出了增长/消减触发器的缺省值和增长/消减的对应值。

民众要领概述

AddItem() 为新元素分派一个空间,把指针添加到二叉树的元素数组中,从而添加.向二叉树中添加一个新元素假如失败,返回负数
RemoveItem() 从二叉树中删除某项. 该项被删除厚,此项上面的所有指针左移一个位置,子项的数目相应地更新,假如nItem在有效的索引范畴内,返回TRUE
FindItem() 抉择利用哪一种查找算法查找元素,假如数组巨细小于对半查找的开始位置,线性查找将被执行,而不是对半查找.
ReSize() 按照nNewSize对二叉树举办增长和消减.假如nNewSize便是当前的数目可能没有更多的内存可供分派了的话返回FALSE,不然返回 TRUE.
Initialise() 在一个工具被建设后,初始化函数必需被挪用.配置内部成员值并为二叉树数组分派空间.
GetSearchMethodThreshold() 获取当前查找算法的临界值.
GetTotalItems() 取恰当前树中存放的子项的数目.
GetTreeSize() 取得树中子项数目标最大值.
GetShrinkTriggerValue() 在消减触发器激活时，返回当前的值
SetShrinkTriggerValue() 配置消减触发器的值.当该树利用的空间与自身的空间百分比小于nPercentageUsed,当且仅当AutoResizing有效时，该树会自动的从头配置子项数目.缺省的消减触发器值为10%
GetShrinkByPercentage() 返回当前消减百分比
SetShrinkByPercentage() 当AutoResize 有效时，配置消减百分比的值.当AutoResize有效而且重设巨细被触发时，该树将会释放nPercentDecrease相关项.
GetGrowTriggerValue() 在增长触发器激活时，返回当前的值
SetGrowTriggerValue() 配置增长触发器的值.当该树已经分派了利用的百分比时,当且仅当AutoResizing有效时，该树会自动的从头配置子项数目.缺省的增长触发器值为90%
GetGrowByPercentage() 返回当前增长百分比
SetGrowByPercentage() 当AutoResize 有效时，配置增长百分比的值.当AutoResize有效而且重设巨细被触发时，该树将会给nPercentIncrease相关项分派空间.
FreeMemory() 释放所有的堆空间，包罗二叉树数组以及个中包罗的子项.用户不必挪用这个函数，除非他想立即释放内存并愿意删除二叉树. 最好的步伐是，利用缺省的析构函数自动的挪用这个函数.
SetSearchMethodThreshold() 配置对半查找的临界值，以区分何时利用对半查找和线性查找。查找要了解按照这个临界值举办切换.缺省值为10.
GetItemPtr() 返回一个空范例指针，用于指向在二叉树子项数组中nItem索引对应的子项的指针.假如索引值超出了有效值，返回空.
GenericLongCompare() 提供应用户的全局较量函数.用来较量两个long型数据（a,b）.假如相等，返回0,假如a<b,返回负数假如 a>b. 返回正数
DoTest() CSimpleBinarySearch类中提供了测试函数.在利用这个函数前，必需先界说BINARY_TREE_EXAMPLE .

本文配套源码

    关键字：

在线提交作业