操作堆排序实现学生后果打点
副标题#e#
1 引言
排序是计较机数据处理惩罚及其它很多软件系统中常用的一种操纵。排序的目标凡是是为了便于查找或为了适应某些查找算法的需要。譬喻,在统计高考后果的系统中,要发生几个表。第一个表按考生的考号从小到大的顺序,列出所有考生的后果;第二个表按考生的测验后果从高到低的顺序,列出所有考生的后果等等。在这样的系统中就要多次举办排序操纵。
排序(Sorting)是把一个无序的数据元素序列按某个要害字举办有序(递增或递减)分列的进程。凡是,待排序的操纵工具称为数据表,它是数据元素(即记录)的有限荟萃。在每一个数据元素中有多个属性。当某个属性用来区分工具作为排序的依据时,该属性就称为排序要害字(Key)。如上例中的考号、测验后果等都是排序要害字。在实际应用中,每个数据表用哪个属性作为排序要害字要视详细的应用需要而定。
排序的要领许多,就其全面的机能而言,很难提出一种被认为是最好的要领,每种要领都各有优缺点,适合在差异的情况下利用。就那时间的机能而言,插入排序、冒泡排序、选择排序机能较量靠近,而快速排序、堆排序、合并排序则是机能较量靠近的另一类。
2 堆排序的道理与技能
堆排序是改造的算法,较量巨大。记录数越多越适合,效率可以明明提高。堆排序是借助于一种称为堆的完全二叉树布局举办排序的,排序进程中,将向量中存储的数据当作是一棵完全二叉树的顺序存储布局,操作完全二叉树中的父结点和子结点之间的内涵干系来选择要害字最小或最大的记录。
详细做法是:把待排序的记录存放在数组r[1‥n]中,将r看作一棵二叉树,每个结点暗示一个记录,第一个记录r[1]作为二叉树的根,今后各记录r[2],…,r[n]依次逐层从左到右顺序分列,组成一棵完全二叉树,任意结点r[i]的左孩子是r[2i],右孩子是r[2i+1],双亲是r[i/2]。对这棵完全二叉树的结点举办调解,使各结点的要害字满意条件,r[i]≤r[2i]且r[i]≤r[2i+1],即每个结点的值均小于或便是它的两个子结点的值,显然在这个堆树中根结点的要害字最小,这种堆被称为“小根堆”。若各结点的值满意r[i]≥r[2i]而且r[i]≥r[2i+1]的堆,称为“大根堆”,大根堆中根结点的要害字值最大。
在堆中,根结点又被称为堆顶元素,当把二叉树转换成大根堆后,堆顶元素最大,把堆顶元素输出,从头调解二叉树的剩余结点,使其成为一个新堆,再输出堆顶元素,便可求得次最大值,如此重复举办,就可获得一个有序序列,这就是操作大根堆排序的根基要领。小堆根的排序要领雷同。
堆排序的要害是结构堆,即调解元素间的干系使之形成堆。由二叉树的性质得知,二叉树中序号最大的一个非终点是[n/2],序号最小的列终结点是序号为1的结点,对这些结点需一一举办调解,使其满意堆的条件。调解进程为:首先把[n/2]号结点元素与其两个孩子中值大者举办较量并互换后,形成以[n/2]为根的子树即为堆,接着用沟通的步调对第[n/2-1]结点举办调解,直至第1个结点。假如在中间调解进程中,由于互换粉碎了以其孩子为根的堆,则要对粉碎了的堆举办调解,依次类推,直到父结点大于便是左、右孩子的元素结点可能孩子结点为空的元素结点。当这一系列调解进程完成时,即成为一个堆树,这个调解进程也叫做“筛选”。
3 堆排序的实现3.1 堆排序在后果打点中的实现
下面给出学生的测验后果表,如图1所示。每条信息由考号与分数构成。以按分数坎坷序次来倾轧每个学生在测验中得到的名次,分数沟通的为同一名次为例,说明堆排序的算法。
这里,二叉树中序号最大的一个非终点是[n/2],即图中的4号结点268.5,序号最小的列终结点是序号为1的结点,即根结点270.0。调解进程为:首先把4号结点元素268.5与其两个孩子中值大者举办较量,由于左孩子272.5>268.5故将它们互换,则以272.5为根的子树即为堆。接着用沟通的步调对第3个结点举办调解,因其满意条件,则不必互换。直至第1个结点270.0,最终形成初始堆,如图3。
#p#副标题#e#
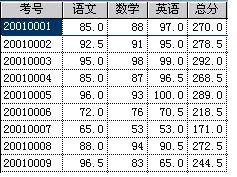
图1 学生测验后果表
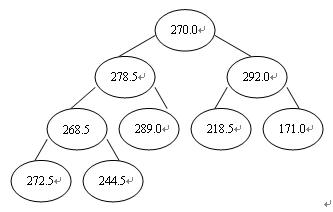
图2 原始数据的二叉树顺序存储形
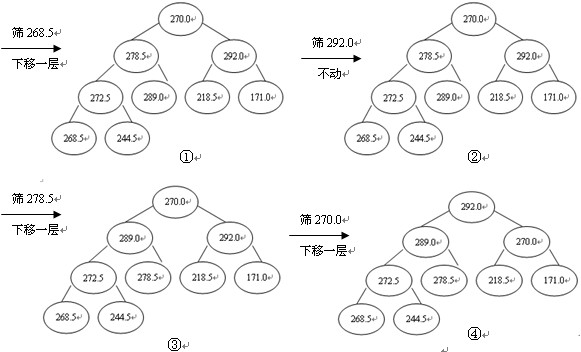
图3 成立初始堆
排序进程为:先输出堆顶元素292.0,把它放到原数组的最后位置,而原数组最后一个单位存放的是244.5,为了不粉碎数据,则把292.0与244.5互换,即r[1]与r[n](n为9)互换,这时r[n]为最大,接着对r[1]与r[n-1]举办筛选又获得新堆,此时新堆的r[1]为当前最大的元素,再把r[1]与r[n-1]对换,使r[n-1]为次最大,这样,颠末n-1次对换、筛选,数组r中的所有元素均按升序分列,堆排序全部完成,如图4所示。
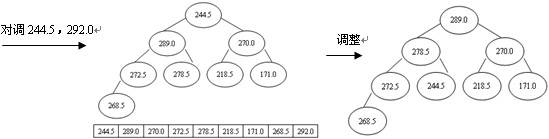
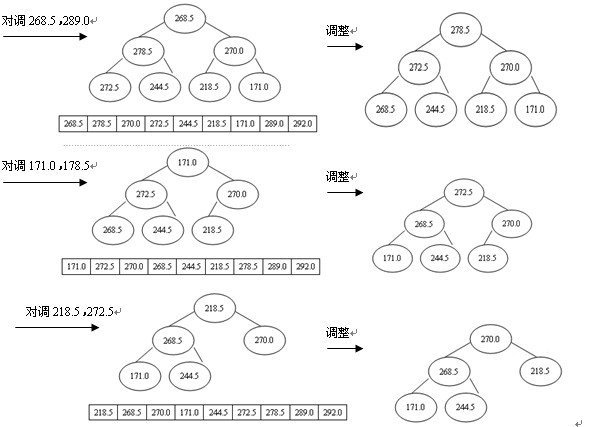
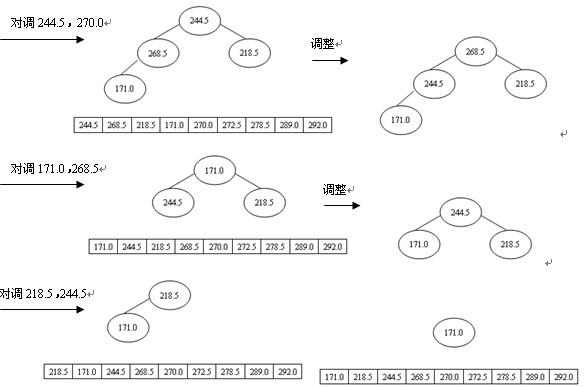
图4 堆排序的进程
3.2 堆排序的算法描写
下面给出整个排序进程及算法描写。(说明:已经有序的子树部门省去。)
#p#分页标题#e#
heapsort (Recordnode r[ ],int n)
{int i,k;
Struct Recordnode x;
For(i=n/2;i>0;i--) /*成立初始堆*/
Sift(r,i,n);
For(i=n;i>1;i--) /*举办n-1次轮回,完成堆排序*/
{ x=r[1]; /*将第一个元素与当前区间的最后一个元素对换*/
r[1]=r[i];
r[i]=x;
sift(r,1,i-1); /*挪用筛选子函数*/
}
}
4 竣事语
从堆排序的算法知道,堆排序所需的较量次数是成立初始堆与从头建堆所需的较量次数之和,其平均时间巨大度和最坏的时间巨大度均为O(n lbn)。它是一种不不变的排序要领。
但对应于大量记录,堆排序的效率却长短常高的。
参考文献
[1](美)Sartaj Sahni ,汪诗林,孙晓东等译.数据布局、算法与应用——C++语言描写.机器家产出书社,2001
[2] 高一凡.《数据布局》算法实现及理会.西安电子科技大学出书社,2004
收稿日期:7月11日 修他日期:8月27日
作者简介:尹聪春(1975-),女,东北财经大学职业技能学院计较机教研室,讲师,研究偏向:计较机网络技能、嵌入式开拓技能。
