C++数组应用之非凡矩阵的压缩存储

副标题#e#

矩阵：

矩阵是数值措施设计中常常用到的数学模子，它是由 m 行和 n 列的数值组成（m=n 时称为方阵）。在用高级语言体例的措施中，凡是用二维 数组暗示矩阵，它使矩阵中的每个元素都可在二维数组中找到相对应的存储位置 。然而在数值阐明的计较中常常呈现一些有下列特性的高阶矩阵，即矩阵中有很 多值沟通的元或零值元，为了节减存储空间，需要对它们举办"压缩存储 "，即不存或少存这些值沟通的元或零值元。

操纵：可以对矩阵作 加、减、乘等运算。

存储压缩方针：

节省存储空间

压缩 的要领：

零元不存储

多个值沟通的只存一个

压缩存储的 工具：

稀疏矩阵

非凡矩阵

非凡矩阵：

值沟通元素 可能零元素漫衍有必然纪律的矩阵称为非凡矩阵 例：对称矩阵、 上（下）三角 矩阵都是非凡矩阵

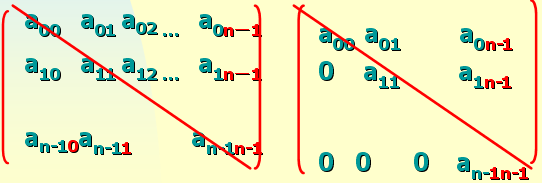
非凡矩阵压缩存储（以对称矩阵为例）

对称矩阵是满意下面条 件的n 阶矩阵： aij= aji　 1<= i，j<= n

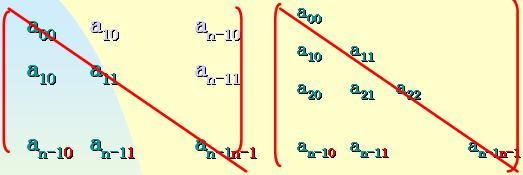
k= 0　　 1　　　 2　　　　 3　　 4　　　　 5　　　 6　　　　　n（n+1）/2-1

#p#副标题#e#

对称矩阵元素可以只存储 下三角部门，共需 n（n+1）/2 个单位的空间（ 三角矩阵的存储方法雷同）

以一维数组sa[0……n（n+1）/2-1]作为n 阶对称矩阵A的 存储布局A中任意一元素 aij与它的存储位置 sa[k] 之间干系：

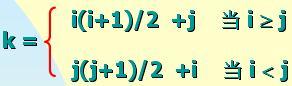
k= 0　　 1　　　 2　　　　 3　　 4　　　　 5　　　 6　　　　　n（n+1）/2-1

譬喻：a42 在 sa[ ]中的 存储位置是：

k=4*（4+1）/2+2=12

sa[12]= a42

带状矩阵 所有非0元素都会合在以主对角线为中心的带状区域，半带宽为d时， 非0元素有 （2d+1）*n-（1+d）*d个（左上角与右下角补上0后，最后必需减掉），如下图 怕示：

#p#副标题#e#

为计较利便，认为每一行都有2d+1个非0元素，若少则0补足存放矩阵 的数组sa[ ]有：n（2d+1）个元素数组，元素sa[k]与矩阵元素aij 之间有干系 ：

k=i*（2d+1）+d+（j-i）（第一项i*（2d+1）暗示前i行一共有几个元 素，d+（j-i）这一项是用来确定第i行中，第j列前有几个元素，以i=j时，这时 j-i=0，这个作为“分水岭”，阁下双方的元素别离加上偏移量d.）

本例：d=1

K= 0　　　 1　　　　　　　　 2　　　　　　　 3　　　　　 4　　　 5　　　　 6　　　　　　　　　　 7　　　 8　　　　 　 9　　　　　 10　　 11　　　 12　　　 13　　　　　 14

（a0前以及a14处放一个0是用来暗示在矩阵的左上角及右下角补上的0 ）

稀疏矩阵：

#p#副标题#e#

行数m = 6， 列数n = 7， 非零元素个数t = 6稀疏矩阵 （SparseMatrix）的抽象数据范例

　template <class Type>
　class SparseMatrix ...{
　　　　　 int Rows, Cols, Terms;　//行/列/非零元素数
　　　　　 Trituple<Type> smArray[MaxTerms];
　public:　//三元组表
　　　　　 SparseMatrix ( int MaxRow, int Maxcol );
　　　　　 SparseMatrix<Type> Transpose ( );　//转置
　　　　　 SparseMatrix<Type>　//相加
　　　　　　　　　　　　　　 Add ( SparseMatrix<Type> b );
　　　　　 SparseMatrix<Type>　//相乘
　　　　　　　　　　　 Multiply ( SparseMatrix<Type> b );
　}

A的三元组顺序表图示

　

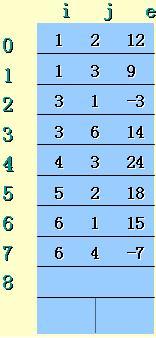
三元组 （Trituple） 类的界说

　template<class Type> class SparseMatrix<Type>;
template<class Type>
　class Trituple ...{
　friend class SparseMatrix <Type>
　private:
　　　　　 int row, col;　//非零元素地址行号/列号
　　　　　 Type value;　//非零元素的值
　}

稀疏矩阵

#p#副标题#e#

转置矩阵

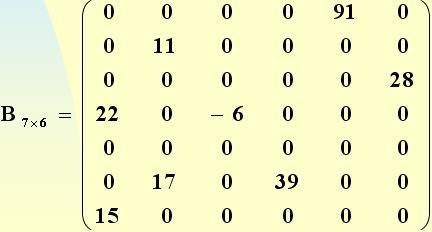
用三元组表暗示的稀疏矩阵及其转置：

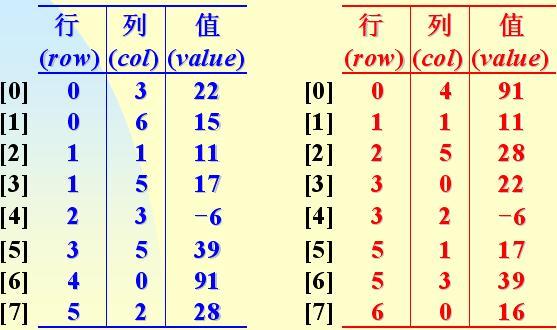
a.smArray　　　　　　　　　　　　　　　　　　　　　　　 　b.smArray

（a.Rows=6,a.Cols=7,a.Terms=8 ）　　　　　　　　　　　 （b.Rows=7,b.Cols=6,b.Terms=8）

#p#副标题#e#

稀疏矩 阵转置算法思想

#p#分页标题#e#

对应上图的一个最简朴的要领是把三元组表中的row与 col的内容交流，然后再凭据新的row中的行号对各三元组从小到大从头排序，最 后获得上图右半部门的三元组表，可是用这样的要领那时间巨大度为平方级的， 下面再用一种要领来处理惩罚：假设稀疏矩阵A有n列，相应地，需要针对它的三元组 表中的col罗列办n次扫描，第k次扫描是在数组的col列中查找列号为k的三元组 ，若找到，则意味着这个三元组所暗示的矩阵元素在稀疏矩阵的第k列，需要把 它存放到转置矩阵的第k行。详细步伐是：取出这个三元组，并互换其row（行号 ）与col（列号）的内容，连同value中存储的值，作为新三元组存放到矩阵的三 元组表中。当n次扫描完成时，算法竣事。措施清单如下：

稀疏矩阵的转 置

　template <class Type> SparseMatrix <Type> SparseMatrix <Type>:: Transpose ( ) ...{
//将稀疏矩阵a(*this指示)转置，功效在稀疏矩阵b中。
　　 SparseMatrix<Type> b ( Cols, Rows );　//建设一 个稀疏矩阵类的工具b
　　　　 b.Rows = Cols; b.Cols = Rows;　//互换其row（行号 ）与col（列号）的内容，连同value
b.Terms = Terms;　//中存储的值作为新三元组放到矩阵的三元组 表中。
　　　　 if ( Terms > 0 ) ...{ //非零元个数不为零
　　　　　　　　 int CurrentB = 0;　//转置三元组表存放指针
for ( int k = 0; k < Cols; k++ )　//按列号做扫描，做 cols次
　　　　　　　　 for ( int i = 0; i < Terms; i++ )　// 在数组中找列号为k的三元组
　　　　　　　　　　　　　　　　 if ( smArray[i].col == k) ...{ //第i个三元组中元素的列号为k
　　　　　　　　　　　　　　　　　 b.smArray[CurrentB].row = k;　//新三元组的行号
　　　　　　　　　　　　　　　　　 b.smArray [CurrentB].col=smArray[i].row;　//新三元组的列号
　　　　　　　　　　　　　　　　　 b.smArray [CurrentB].value=smArray[i].value;　//新三元组的值
　　　　　　　　　　　　　　　　 CurrentB++;　//存放指针加 1
　　　　　　　　　　　　　　 }
　　　　 }
　　　　 return 0;
　}

若设稀疏矩阵的行数为Rows，列数为Cols，非 零元素个数为Terms，则最坏环境下的时间巨大度主要取决于二重潜套for轮回内 的if语句，if语句在二重轮回的浸染下总的执行次数为O（Cols*Terms）。而在 if节制内的赋值语句则执行了Terms次，它取决于三元组表自己的长度。若非零 元素个数Terms与矩阵行，列数的乘积Rows*Cols等数量级，则上述措施清单的时 间巨大度为O（Cols*Terms）＝O（Rows*Cols*Cols）。设Rows=500，Cols=100， Terms=10000，则O（500*100*100）=O（5000 000），处理惩罚效率极低。

为 了提高转置效率，回收一种快速转置的要领。在此要领中，引入两个帮助数组：

1. rowSize[].用它存放事先统计出来的稀疏矩阵各列的非零元素个数， 转置今后是转置矩阵各行的非零元素个数。详细做法是：先把这个数组清零，然 后扫描矩阵A的三元组表，逐个取出三元组的列号col，把以此列号为下标的帮助 数组元素的值累加1.

for（int i=0；i<Cols；i++） rowSize[i]=0； //清零

for（j=0；j<Terms；j++） rowSize[smArray[j].col]++；// 统计，留意这里用到的简捷的算法

2. rowstart[].用它存放事先计较出 来的稀疏矩阵各行非零元素在转置矩阵的三元组表中应存放的位置。

rowSize[0]=0；//计较矩阵b第i行非零元素的开始存放位置

for （i=1；i<Cols；i++）rowStart[i]=rowStart[i-1]+rowSize[i-1]

快 速转置算法的思想

·成立帮助数组 rowSize 和 rowStart，记录 矩阵转置后各行非零元素个数和各行元素在转置三元组表中开始存放位置。

·扫描矩阵三元组表，按照某项的列号，确定它转置后的行号， 查 rowStart 表，按查到的位置直接将该项存入转置三元组表中。

·转置时间价钱为O（max（Terms， Cols））。若矩阵有200 列 ，10000个非零元素，总共需要10000次处理惩罚。

#p#副标题#e#

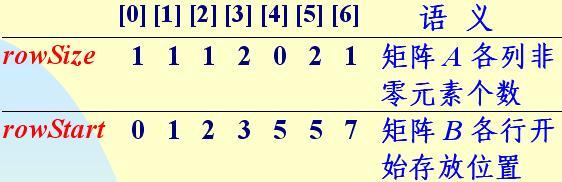
对应上图的代码在就像前面所列的：

for （ int i = 0 ； i < Cols； i++ ） rowSize[i] = 0；

for （ i = 0； i < Terms； i++ ）

rowSize[smArray[i].col]++；

rowStart[0] = 0 ；

for （ i = 1； i < Cols； i++ ）

rowStart[i] = rowStart[i-1]+rowSize[i-1]；

稀疏矩阵的快速转置

#p#分页标题#e#

　 template <class Type> SparseMatrix<Type>
SparseMatrix<Type>::FastTranspos ( ) ...{
//对稀疏矩阵a(*this指示)做快速转置，功效放在b中，时间价钱 为O(Terms+Columns)。
　　　 int *rowSize = new int[Cols];　//帮助数组，统计各列 非零元素个数
　　　 int *rowStart = new int[Cols];　//帮助数组，估量转 置后各行存放位置
　　　 SparseMatrix<Type> b ( Cols, Rows );　//存放 转置功效
　　　 b.Rows = Cols;　　 b.Cols = Rows;
　　 b.Terms = Terms;
　　　 if ( Terms > 0 ) ...{
　　　　　　　 for (int i = 0; i < Cols; i++) rowSize [i] = 0;　//统计矩阵b中第i行非零元素个数
for ( i = 0; i < Terms; i++ )
//按照矩阵a中第i个非零元素的列号，将rowSize相当该列的计数 加1
　　　　　　　 rowSize[smArray[i].col]++;
rowStart[0] = 0;　//计较矩阵b第i行非零元素的开始存放位置
　　　　　　　　 for ( i = 1; i < Cols; i++ ) 　//rowStart[i]=矩阵b的第i行的开始存放位置
　　　　　　　　　　 rowStart[i] = rowStart[i-1]+rowSize [i-1];
　　　　　　 for ( i = 0; i < Terms; i++ ) ...{　　　　 　 //从a向b传送
　　　　　　　　　　 int j = rowStart[smArray[i].col]; 　//j为第i个非零元素在b中应存放的位置
　　　　　　　　　　 b.smArray[j].row = smArray[i].col;
　　　　　　　　　　 b.smArray[j].col = smArray[i].row;
　　　　　　　　　　 b.smArray[j].value = smArray [i].value;
　　　　　　　　　　 rowStart[smArray[i].col]++;
　　　　　　 }
　　　 }
　　　 delete[ ] rowSize;　　 delete [ ] rowStart;
　　　 return b;
}

在此措施中有4个并列轮回，那时间巨大度别离为 O（Cols），O（Terms），O（Cols），和O（Terms），则措施总的时间巨大度为 O（Cols+Terms）。当Terms与Rows*Cols等数量级时，措施的时间巨大度为O （Cols＋Terms）＝O（Rows*Cols）。设Rows=500，Cols＝100，Terms=10000， 则O（500*100）=O（50000）。当Terms远远小于Rows*Cols时，此措施会更省时 间，但措施中需要增加两个别积为Cols的帮助数组。一般Terms老是大于Cols的 ，假如可以或许大幅度提高速度，这点空间存储上的开销是值得的。