可设置语法阐明器开拓纪事(五) 结构一个真正能用的状态机(中)
副标题#e#
上一篇博客写到了如何给一个非终结符的文礼貌则结构出一个压缩过的下推状态机,那么本日说的就是如何把所有的文法都毗连起来。其实主要的idea在(三)和他的勘误(三点五)内里已经说得差不多了。可是本日我们要处理惩罚的是带信息的transition,所以尚有一些处所要留意。
所以在这里我们先把几条文法的最后的状态机都列出来(大图):
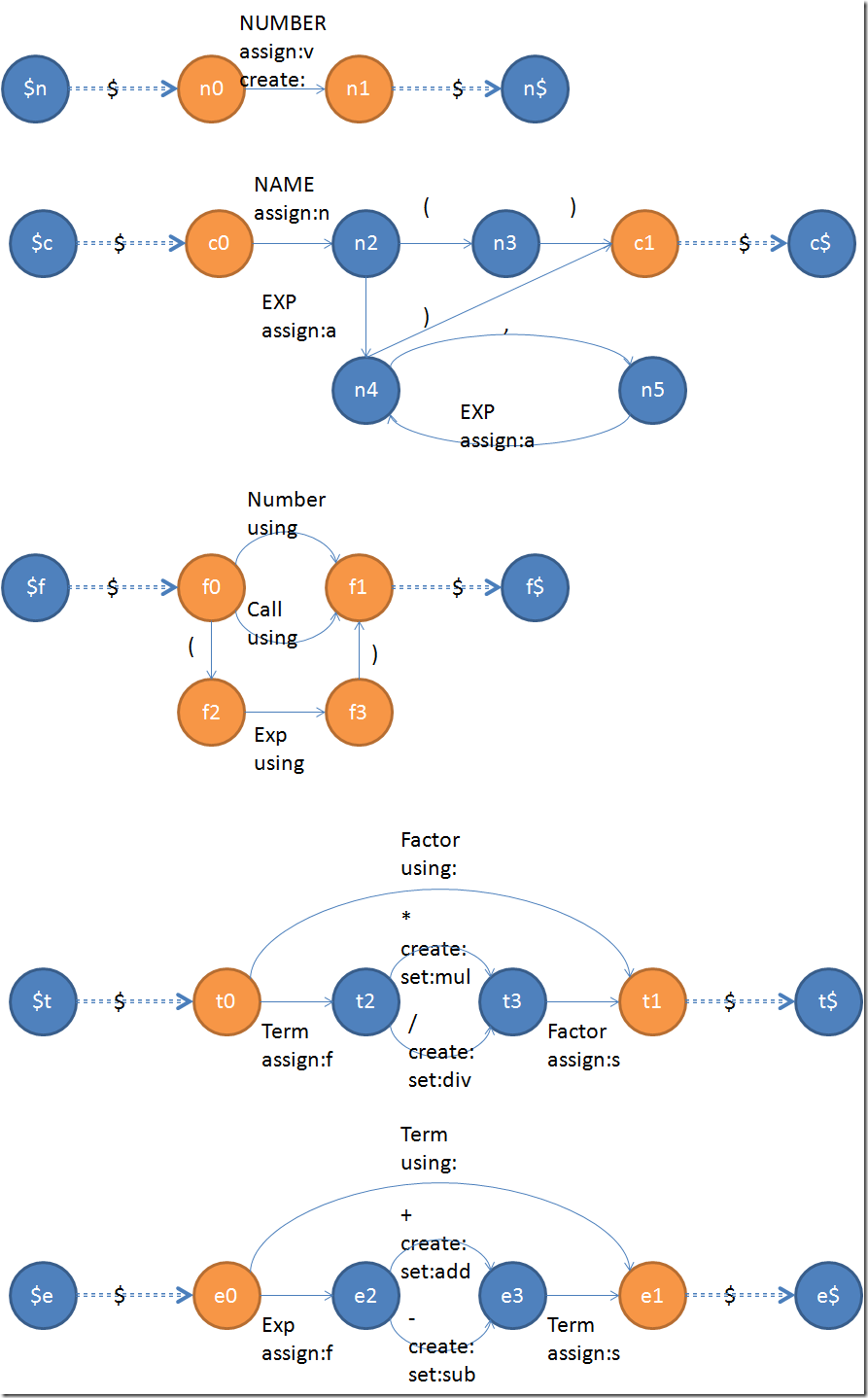
本栏目
#p#副标题#e#
接下来的这一步,就是要对所有靠非终结符(Exp啊Term这些)举办跳转的transition都执行上一篇文章所说的传说中的交错链接。在发生链接的时候,我们给shift和reduce的边别离加上shift和reduce。而shift和reduce是有参数的——就是被shift走的状态的id。这样可以在parse的时候匹配和处理惩罚状态仓库。在这里我门对e3->e1这一步做一下操纵做为例子。赤色的边是被删掉的,而粗壮的绿色边是被新加进去的:
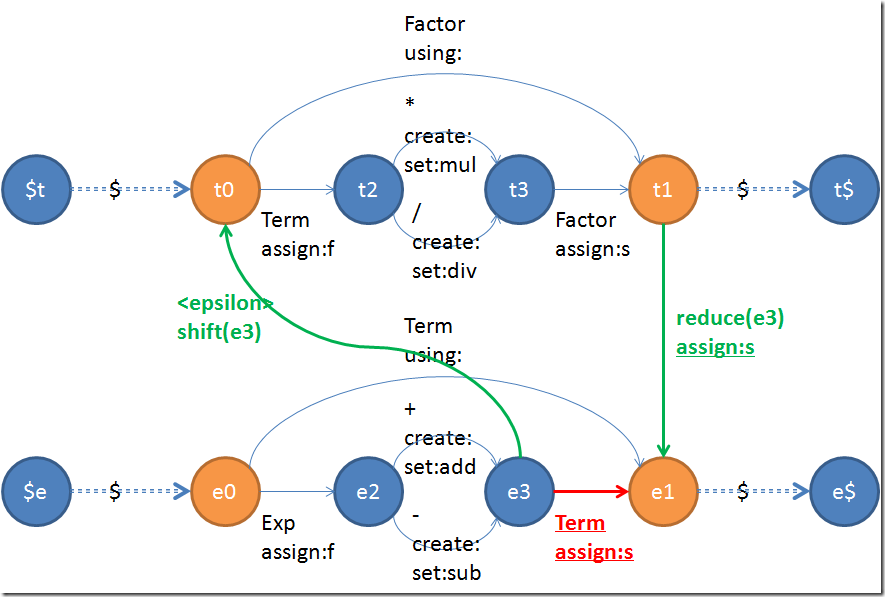
赤色的边酿成了两条绿色的边,赤色的边附带的信息则被复制到了绿色的reduce边上。当我们利用这个状态机的时候,shift(s3)就暗示往仓库内里压入s3,reduce(s3)就暗示从仓库内里弹出(s3)。虽然弹出不必然会乐成,所以假如不乐成的话,这条边就不能在其时利用。因此这也就是为什么在e3跳转到t0之后,t1知道往回跳的是e1而不是此外什么处所——就如同为什么C++的函数执行完之后老是知道如何跳转回挪用它的处所一样——因为把信息推入了仓库。
本栏目
那此刻我们就来看一下,当所有的非终结符跳转都处理惩罚掉之后,会酿成什么样子吧(这个图真是巨大和乱到我不想画啊),为了让图变得不那么糟糕,我把shift都酿成紫色,reduce都酿成绿色:
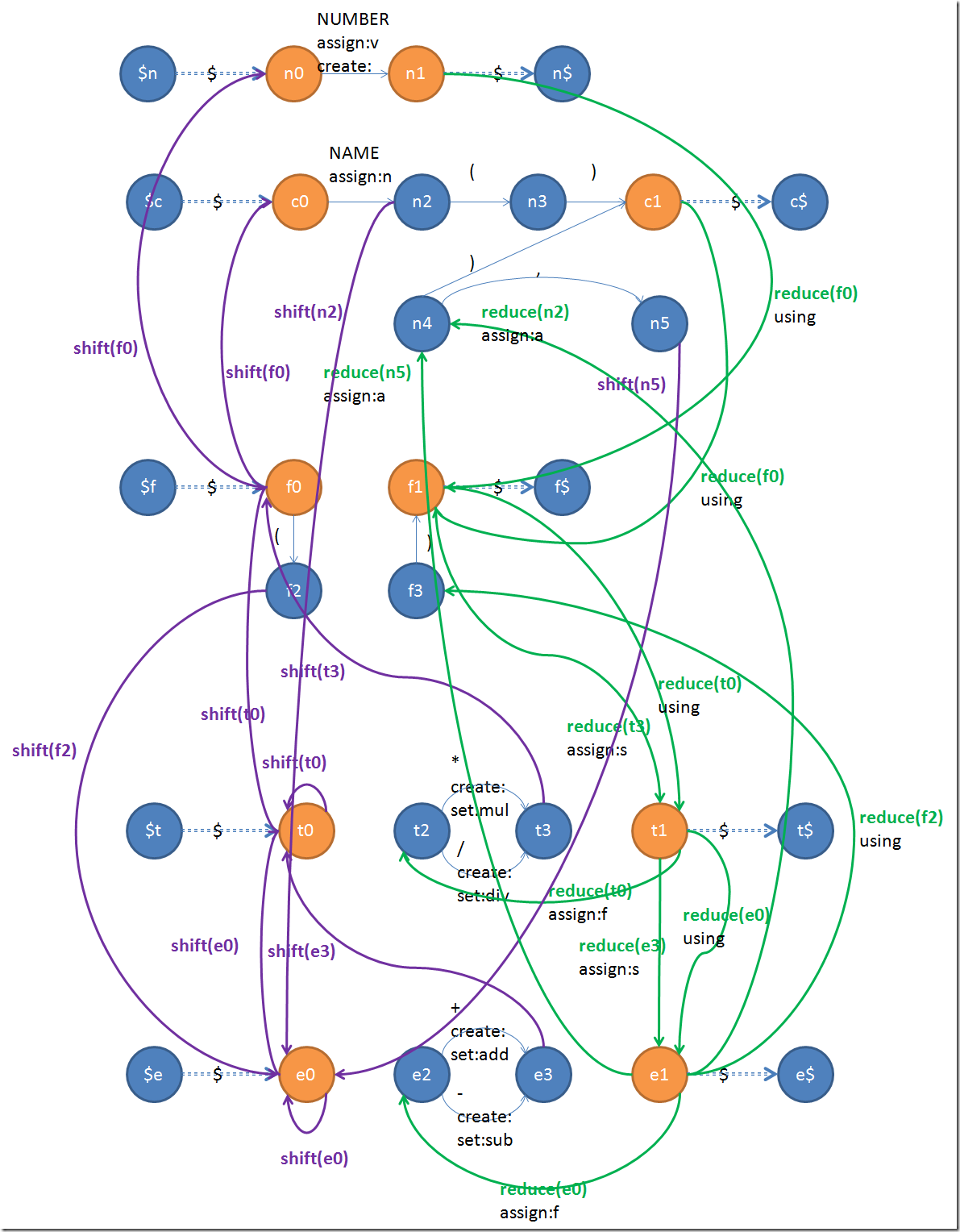
在添加shift和reduce边之前,每一条边都是有输入token的。可是我们方才添加上去的shift和reduce边却是不输入token的,所以他们是epsilon边,下一步就是要消除他们。上面这个图消除了epsilon边之后,会酿成一个状态很少,可是每一条边附带的信息城市很是多,并且像n1这种常常达到的状态(因为四则运算内里有很大都字)将规复射出无数条边。到了这里这个状态机已经再也画不出来了。所以我下面就只拿两个例子来画。下面要展示的是用Exp来parse单独的一个数字会走的边,虽然就是Exp –> Term –> Factor –> Number了:
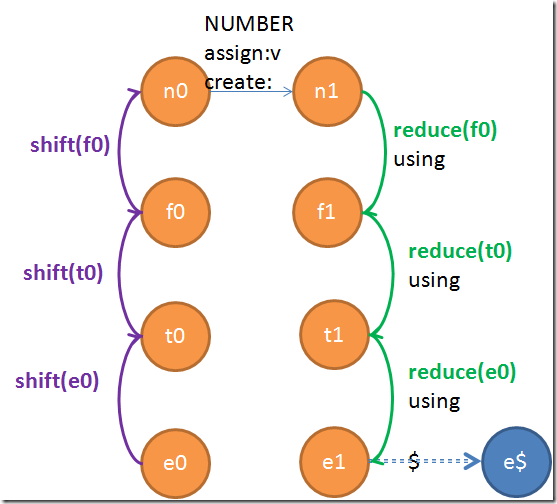
就会被处理惩罚成:
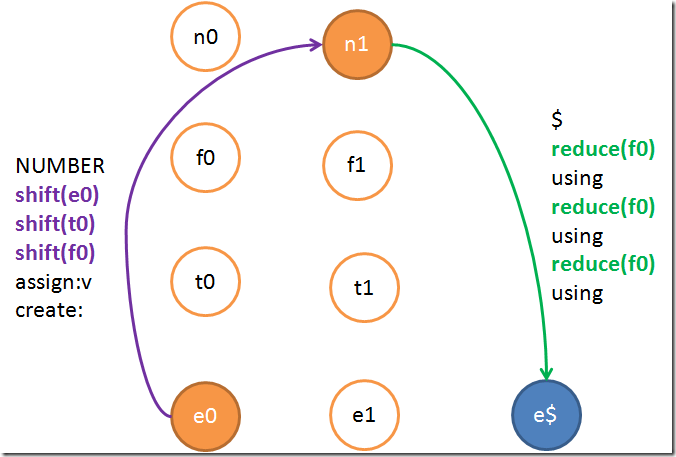
留意边上面的信息是要按顺序从头叠加在一起的。当所有的epsilon边都去掉了之后,我们就获得了最终的一个状态机。最重要的一件工作呈现了。我们知道,发现LR和LALR这种对象就根基上是为了处理惩罚左递归的,所以这种图就可以在去除epsilon边的进程中自动发明左递归。这是怎么做到的呢?只要在去除epsilon边的时候,发明白一条完全由shift这种epsilon边构成的环,那么左递归就发明白。为了利便,我们可以只处理惩罚直接左递归——就是这种环的长度是1的。不包括间接左递归的问法是很容易写出来的。虽然这种环并不必然是首尾相接的,譬如说我们在处理惩罚e0的时候就会发明e0->t0->t0这种环(虽然严格来说环只有最后一截的这个部门)。我们的措施要很好地应对这种环境。因为我们只接管直接左递归,所以雷同这种布局的epsilon路径可以直接的丢弃他,因为t0->t0会被t0状态单独处理惩罚掉。因此这样做并不会遗漏什么。
细心的伴侣大概会发明,这个布局的图是不能直接处理惩罚右递归的(总之左递归和右递归总要有一个会让你的状态机傻逼就是了!)。关于如那里理惩罚有递归(其实内容也不巨大)处所法会在“下篇”描写出来。那处理惩罚左递归有什么用呢?举个例子,我们的e0->e2就是一个左递归,而他会在之前的步调被处理惩罚成shift(e0->e0)和reduce(e1->e2)。我们要记下shift和reduce的对应干系,那么当我们找到一个左递归的shift之后,我们就可以把对应的reduce给标志成“left-recursive-reduce”。这是一个在结构语法树的时候,很是要害的一种结构指令。
处理惩罚完这些之后,我们可以把左递归的shift边全部删掉,最后把token和state都统统处理惩罚成持续的数字,做成一张[state, token] –> [transitions]的二维表,每一个表的元素是transition的列表。为什么是这样呢?因为我们对一个state输入一个token之后,由于生存着state的仓库(你还记得吗?shift==push,reduce==pop)的栈顶若干个元素的差异,大概会走不通的蹊径。于是最后我们就获得了这么一张图。
#p#分页标题#e#
下面这张图可以通过运行gac.codeplex.com上面的Common\UnitTest\UnitTest.sln(VS2012限定)之后,在Common\UnitTest\TestFiles\Parsing.Calculator.Table.txt内里找到。这一组文件都是我在测试状态机的时候log下来的。
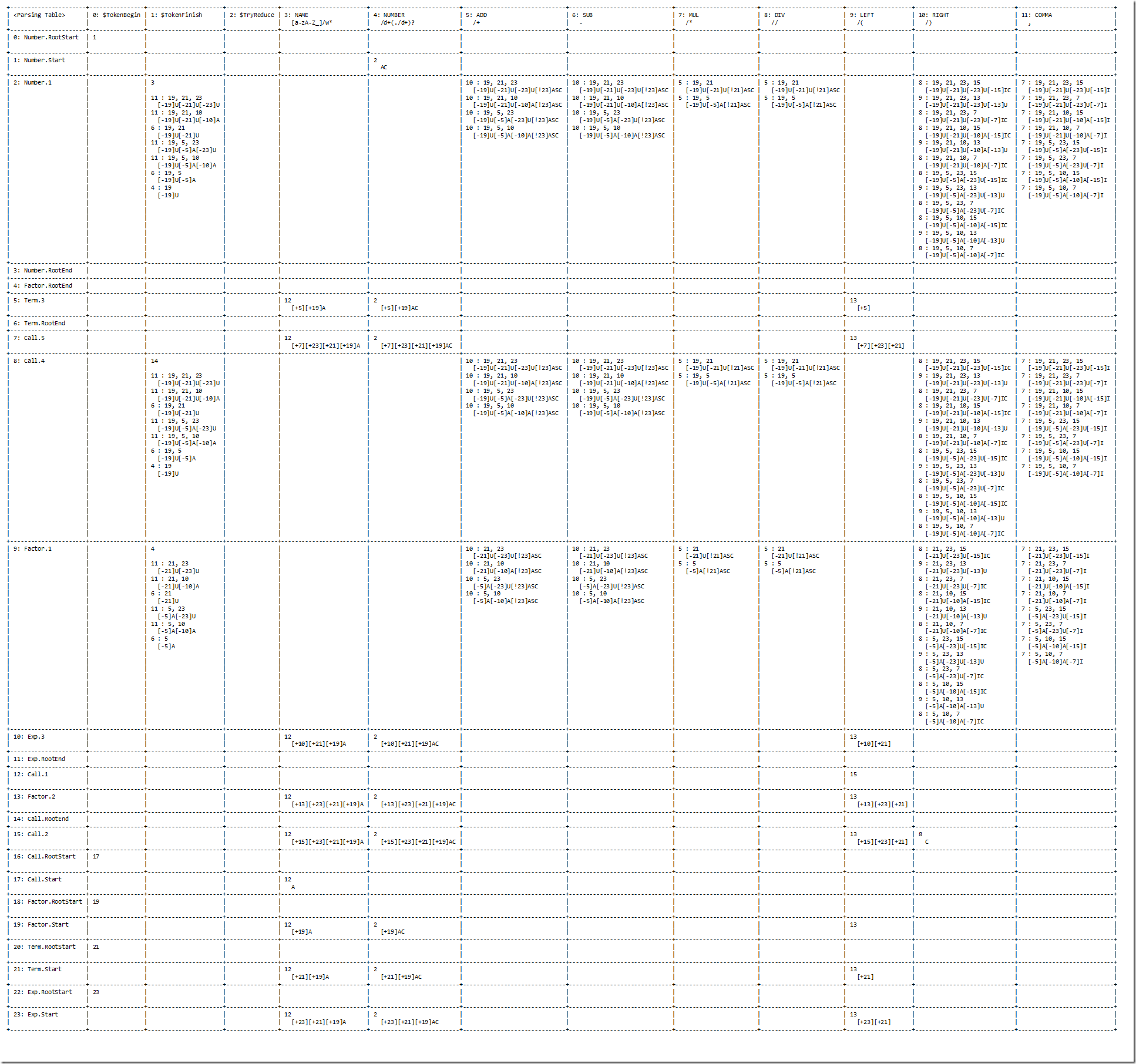
假如各人有VS2012的话,通过运行我筹备的几个输入,譬如说“1*2+3*4”,就可以在Parsing.Calculator.[2].txt内里找到所有状态跳转的轨迹。因为我们老是需要parse一个Exp,所以我们从22: Exp.RootStart开始。我们假设token stream的第一个和最后一个体离是$TokenBegin和$TokenFinish。上图的$TryReduce是为了应对右递归而设计出来的一种非凡输入。由于四则运算内里并没有右递归,所以这一列就是空的:
StartState: 22[Exp.RootStart]
$TokenBegin => 23[Exp.Start]
State Stack:
NUMBER[1] => 2[Number.1]
State Stack: 23[Exp.Start], 21[Term.Start], 19[Factor.Start]
Shift 23[Exp]
Shift 21[Term]
Shift 19[Factor]
Assign value
Create NumberExpression
MUL[*] => 5[Term.3]
State Stack: 23[Exp.Start]
Reduce 19[Factor]
Using
Reduce 21[Term]
Using
LR-Reduce 21[Term]
Assign firstOperand
Setter binaryOperator = Mul
Create BinaryExpression
NUMBER[2] => 2[Number.1]
State Stack: 23[Exp.Start], 5[Term.3], 19[Factor.Start]
Shift 5[Term]
Shift 19[Factor]
Assign value
Create NumberExpression
ADD[+] => 10[Exp.3]
State Stack:
Reduce 19[Factor]
Using
Reduce 5[Term]
Assign secondOperand
Reduce 23[Exp]
Using
LR-Reduce 23[Exp]
Assign firstOperand
Setter binaryOperator = Add
Create BinaryExpression
NUMBER[3] => 2[Number.1]
State Stack: 10[Exp.3], 21[Term.Start], 19[Factor.Start]
Shift 10[Exp]
Shift 21[Term]
Shift 19[Factor]
Assign value
Create NumberExpression
MUL[*] => 5[Term.3]
State Stack: 10[Exp.3]
Reduce 19[Factor]
Using
Reduce 21[Term]
Using
LR-Reduce 21[Term]
Assign firstOperand
Setter binaryOperator = Mul
Create BinaryExpression
NUMBER[4] => 2[Number.1]
State Stack: 10[Exp.3], 5[Term.3], 19[Factor.Start]
Shift 5[Term]
Shift 19[Factor]
Assign value
Create NumberExpression
$TokenFinish => 11[Exp.RootEnd]
State Stack:
Reduce 19[Factor]
Using
Reduce 5[Term]
Assign secondOperand
Reduce 10[Exp]
Assign secondOperand
本栏目
我们把所有跳转过的transition的信息都记录下来,就可以结构语法苏了。我们想象一下,在执行这些指令的时候,碰着NUMBER[4]就便是得到了一个内容为4的token,shift的话就是往仓库内里push进一个状态的名字,而reduce则是弹出。
相对应的,因为每一个文法城市建设一个工具,所以我们在初始化的时候,要先放一个空工具在仓库上。shift一次就再建设一个空的工具push进去,reduce的时候就把栈顶的工具弹出来作为“待处理惩罚工具”,using了就把待处理惩罚工具和栈顶工具归并,left-reduce就是把栈顶工具弹出来作为待处理惩罚工具的同时,push一个空工具进去。assign fieldName就是把“待处理惩罚工具”生存到栈顶工具的叫做fieldName的成员变量内里去。假如栈顶工具为空,那么被生存的工具就是方才输入的谁人token了。因此我们从新到尾执行一遍之后,就可以获得下面的一颗语法树:
BinaryExpression {
binaryOperator = [Add]
firstOperand = BinaryExpression {
binaryOperator = [Mul]
firstOperand = NumberExpression {
value = [1]
}
secondOperand = NumberExpression {
value = [2]
}
}
secondOperand = BinaryExpression {
binaryOperator = [Mul]
firstOperand = NumberExpression {
value = [3]
}
secondOperand = NumberExpression {
value = [4]
}
}
}
根基上parsing的进程就竣事了。在“下篇”——也就是(六)——内里,我会报告如那里理惩罚右递归,然后这个系列根基上就要完结了。
